题目内容
5.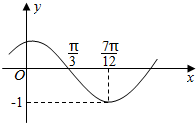 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<ϕ<π)的图象如图所示,为了得到g(x)=Asinωx的图象,可将f(x)的图象( )
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<ϕ<π)的图象如图所示,为了得到g(x)=Asinωx的图象,可将f(x)的图象( )| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式,再利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:根据函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<ϕ<π)的图象,
可得A=1,$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,求得ω=2.
再根据五点法作图可得,2×$\frac{π}{3}$+φ=π,求得φ=$\frac{π}{3}$.
故f(x)=sin(2x+$\frac{π}{3}$),故把f(x)的图象向右平移$\frac{π}{6}$个单位,可得g(x)=sin2x的图象,
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
15.已知球O的表面积为12π,则球O的体积为( )
| A. | 2$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 12$\sqrt{3}$π | D. | 32$\sqrt{3}$π |
10.下列函数中,即是奇函数又是定义域内的增函数的是( )
| A. | $y=-\frac{1}{x}$ | B. | y=|x+1|-1 | C. | y=x|x| | D. | y=x2 |
17.设函数$f(x)=\left\{{\begin{array}{l}{({k-1}){x^2}-3({k-1})x+\frac{13k-9}{4},x≥2}\\{{{({\frac{1}{2}})}^x}-1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x<2}\end{array}}\right.$,若f(n+1)<f(n)对于一切n∈N+恒成立,则实数k的取值范围为( )
| A. | $k<-\frac{1}{5}$ | B. | $\frac{2}{5}≤k<1$ | C. | $k≤-\frac{2}{5}$ | D. | k<1 |