题目内容
已知函数f(x)=| 1 |
| x2+1 |
| 1 |
| x |
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
| x | … | |||||||
f(x)-
|
… | |||||||
g(x)-
|
… |
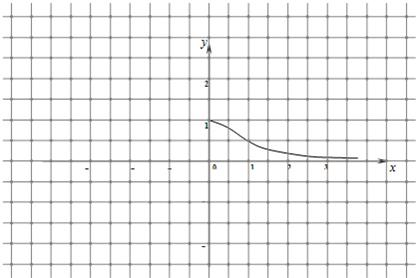
分析:(1)先由条件,f(x)的定义域为一切实数,故x2≥0,从而得出函数的值域;
(2)由表格内数据猜想:f(x)-
=-(g(x)-
)或f(x)+g(x)=1,从而得出函数f(x)和g(x)都是偶函数,其本身图象关于y轴对称.
(3)由于f(x)-
=-(g(x)-
),所以函数f(x)-
的图象和g(x)-
的图象关于x轴对称,即f(x)图象和g(x)图象关于直线y=
对称.由此,可作出f(x)和g(x)在定义域内的全部图象.
(2)由表格内数据猜想:f(x)-
| 1 |
| 2 |
| 1 |
| 2 |
(3)由于f(x)-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: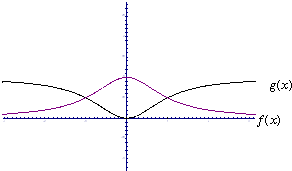 解:(1)由条件,f(x)的定义域为一切实数,故x2≥0
解:(1)由条件,f(x)的定义域为一切实数,故x2≥0
所以,f(x)∈(0,1].
(2)表格内数据只要满足f(x)-
和g(x)-
互为相反数即可得分.
猜想:f(x)-
=-(g(x)-
)或f(x)+g(x)=1
证明:f(x)+f(
)=
+
=1
(3)f(x)和g(x)的图象见下图.
因为x∈R,且f(-x)=f(x),g(-x)=g(x),所以函数f(x)和g(x)都是偶函数,其本身图象关于y轴对称.
(注:只作对f(x)图象,并说明了理由的可得2分)
∵f(x)-
=-(g(x)-
)所以函数f(x)-
的图象和g(x)-
的图象关于x轴对称,即f(x)图象和g(x)图象关于直线y=
对称.
由此,可作出f(x)和g(x)在定义域内的全部图象.
 解:(1)由条件,f(x)的定义域为一切实数,故x2≥0
解:(1)由条件,f(x)的定义域为一切实数,故x2≥0所以,f(x)∈(0,1].
(2)表格内数据只要满足f(x)-
| 1 |
| 2 |
| 1 |
| 2 |
猜想:f(x)-
| 1 |
| 2 |
| 1 |
| 2 |
证明:f(x)+f(
| 1 |
| x |
| 1 |
| x2+1 |
| x2 |
| 1+x2 |
(3)f(x)和g(x)的图象见下图.
因为x∈R,且f(-x)=f(x),g(-x)=g(x),所以函数f(x)和g(x)都是偶函数,其本身图象关于y轴对称.
(注:只作对f(x)图象,并说明了理由的可得2分)
∵f(x)-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由此,可作出f(x)和g(x)在定义域内的全部图象.
点评:此题考查了函数解析式的求解及常用方法,还考查了函数的值域,此题解答的关键是数形结合思想的运用.

练习册系列答案
相关题目