Question

【题目】四棱锥P﹣ABCD的顶点P在底面ABCD上的投影恰好是A，其正视图与侧视图都是腰长为a的等腰直角三角形．则在四棱锥P﹣ABCD的任意两个顶点的连线中，互相垂直的异面直线共有 对．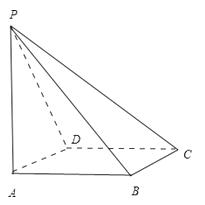

Answer 1

【答案】8
【解析】解：∵四棱锥P﹣ABCD的顶点P在底面ABCD上的投影恰好是A，
其正视图与侧视图都是腰长为a的等腰直角三角形，
∴四棱锥P﹣ABCD中，PA⊥面ABCD，ABCD是边长为a的正方形，PA=a，（如图）
∴在四棱锥P﹣ABCD的任意两个顶点的连线中，互相垂直的异面直线有：
PA和CD，PA和BC，PA和BD，PD和AB，PB和AD，PC和BD，PD和BC、PB和CD，共8对．
所以答案是：8．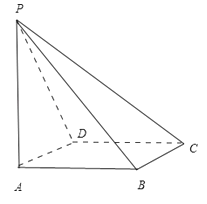

【考点精析】利用简单空间图形的三视图和异面直线的判定对题目进行判断即可得到答案，需要熟知画三视图的原则：长对齐、高对齐、宽相等；过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.（不在任何一个平面内的两条直线）．