题目内容
已知O为平面直角坐标系的原点,过点M(-2,0)的直线l与圆x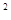 +y
+y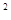 =1交于P、Q两点,且
=1交于P、Q两点,且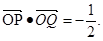
(Ⅰ)求∠PDQ的大小;
(Ⅱ)求直线l的方程.
【答案】
(Ⅰ)∠POQ=120°.(Ⅱ) 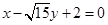 或
或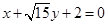 .
.
【解析】
试题分析:(Ⅰ)因为P、Q两点在圆x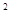 +y
+y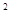 =1上,所以
=1上,所以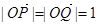 ,
,
因为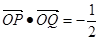 ,
,
所以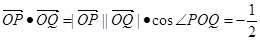 .
.
所以∠POQ=120°. 5分
(Ⅱ)依题意,直线l的斜率存在,
因为直线l过点M(-2,0),可设直线l:y=k(x+2).
由(Ⅰ)可知O到直线l的距离等于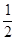 .
.
所以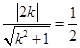
得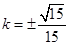
所以直线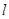 的方程为
的方程为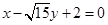 或
或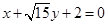 9分
9分
考点:直线与圆的位置关系,直线方程,平面向量的数量积。
点评:中档题,中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。恰当的运用圆中的“特征三角形”,转化成点到直线的距离问题,更为简洁。

练习册系列答案
相关题目
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.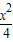 +
+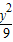 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.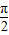 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 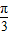 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.