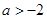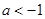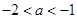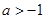题目内容
已知函数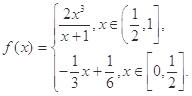
函数
，若存在
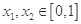，使得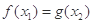
成立，则实数a的取值范围是 ．
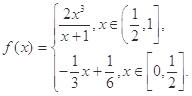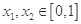函数，若存在，使得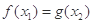成立，则实数a的取值范围是 ．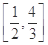
试题分析：当x∈
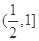时，f(x)=
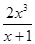值域是(0，1]，当x∈
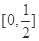时，f(x)=
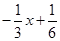值域是[0，
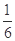]，故函数
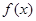在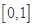
的值域为[0，1]，又根据三角函数的有界性得值域是[2-2a，2-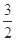
a]，∵存在存在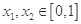，使得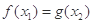成立，∴[0，1]∩[2-2a，2-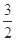a]≠∅，若[0，1]∩[2-2a，2-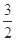a]=∅，则2-2a＞1或2-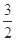a＜0，即a＜
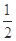或a＞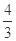
,∴a的取值范围是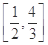．点评：解题的关键是通过看两函数值域之间的关系来确定a的范围
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
g(x)恒成立，求实数a的取值范围．
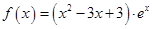，设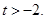
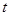的取值范围，使得函数
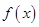在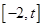
上为单调函数；
.
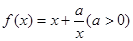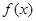在定义域上的单调性；
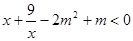在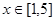
上恒成立时的实数
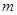的取值范围？
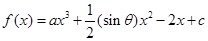的图象过点
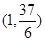，且在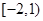
内单调递减，在
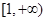上单调递增。
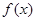的解析式；
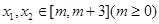，不等式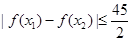
恒成立，试问这样的
是否存在.若存在，请求出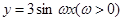
在区间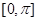
恰有2个零点，则
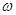的取值范围是( )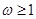
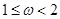
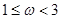
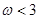
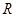上的函数
是最小正周期为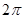
的偶函数，当
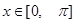时，
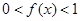，且在
上单调递减，在
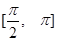上单调递增，则函数
在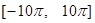
上的零点个数为 ．
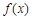满足
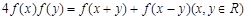，且
，
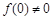，则下列等式不成立的是（ ）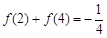
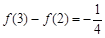
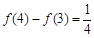
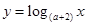在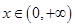
上是减函数，则
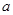的取值范围是
