题目内容
已知数列{an}的前n项和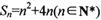 ,数列
,数列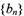 为等比数列,且首项b1和公比q满足:
为等比数列,且首项b1和公比q满足: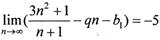
(I)求数列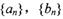 的通项公式;
的通项公式;
(II)设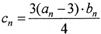 ,记数列
,记数列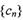 的前n项和
的前n项和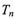 ,若不等式
,若不等式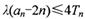 对任意
对任意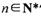 恒成立,求实数
恒成立,求实数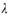 的最大值.
的最大值.
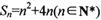 ,数列
,数列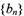 为等比数列,且首项b1和公比q满足:
为等比数列,且首项b1和公比q满足: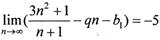
(I)求数列
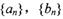 的通项公式;
的通项公式;(II)设
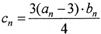 ,记数列
,记数列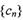 的前n项和
的前n项和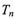 ,若不等式
,若不等式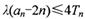 对任意
对任意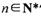 恒成立,求实数
恒成立,求实数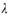 的最大值.
的最大值.(Ⅰ)当n=1时,a1=S1=5.
当n≥2时an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,
验证n=1时也成立.
∴数列{an}的通项公式为:an=2n+3(n∈N*).
∵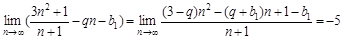
∴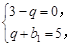 解得:b1=2,q=3.
解得:b1=2,q=3.
∴数列{bn}的通项公式为:bn=2·3n-1.……………………………………5分
(Ⅱ)∵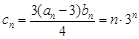 ,
,
∴ Tn= c1+ c2+ c3+…+ cn
=3+2·32+3·33+……+n·3n················ ①
3Tn=32+2·3n+3·34+……+n·3n+1·············· ②
由①-②得:-2Tn=3+32+……+3n-n·3n+1
=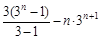
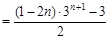 ,
,
∴ .………………………………………………………8分
.………………………………………………………8分
不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)·3n+1,(*)
设f (n)=(2n-1)·3n+1,
(n)=(2n-1)·3n+1,
易知函数f (n)在n∈N*上单调递增,
故当n=1时(2n-1)·3n+1取得最小值为4,
∴由题意可知:不等式(*)对一切n∈N*恒成立,只需λ≤4.
∴实数λ的最大值为4.
当n≥2时an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,
验证n=1时也成立.
∴数列{an}的通项公式为:an=2n+3(n∈N*).
∵
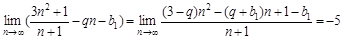
∴
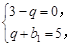 解得:b1=2,q=3.
解得:b1=2,q=3. ∴数列{bn}的通项公式为:bn=2·3n-1.……………………………………5分
(Ⅱ)∵
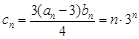 ,
,∴ Tn= c1+ c2+ c3+…+ cn
=3+2·32+3·33+……+n·3n················ ①
3Tn=32+2·3n+3·34+……+n·3n+1·············· ②
由①-②得:-2Tn=3+32+……+3n-n·3n+1
=
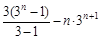
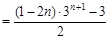 ,
,∴
 .………………………………………………………8分
.………………………………………………………8分不等式λ(an-2n)≤4Tn可化为λ≤(2n-1)·3n+1,(*)
设f
 (n)=(2n-1)·3n+1,
(n)=(2n-1)·3n+1,易知函数f (n)在n∈N*上单调递增,
故当n=1时(2n-1)·3n+1取得最小值为4,
∴由题意可知:不等式(*)对一切n∈N*恒成立,只需λ≤4.
∴实数λ的最大值为4.
略

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
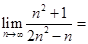 ___________.
___________.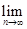
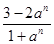 的值是 .
的值是 .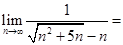 。
。 ,an+an+1=
,an+an+1= ,则
,则 (a1+a2+…+an) = ( )
(a1+a2+…+an) = ( )
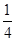

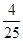
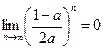 ,则a的取值范围是( )
,则a的取值范围是( )
 或
或

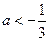 或
或
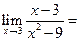
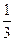
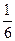
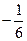
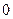
 。
。