题目内容
已知A、B、C、D是同一球面上的四点，且每两点间距离都等于2，则球心到平面BCD的距离是( )A.
B．
C．
D．
C
解析：本题考查组合体的运算及空间想象能力；据题意同一球面上的四点A、B、C、D可构成球的内接正四面体，而正四面体可看成是球的内接正方体的面对角线构成的几何体，此时正方体的边长为，那么由正方体的体对角线即为球的直径2R：(2R)2=()2+()2+(
)2
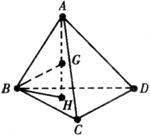
R=
，此时设球的球心为G，如图在正四体ABCD中，A在底面BCD的射影为H，其中GB=R，BH=
，在直角三角形GBH中易得GH=
．
练习册系列答案
相关题目