题目内容
已知A、B、C、D是球面上四点，若AB=AC=
，BD=DC=CB=2，二面角A-BC-D的平面角等于150°，则该球的表面积为（ ）
| 2 |
分析：由题设知四面体ABCD中，AB=AC=
，BD=DC=CB=2，设等边△BDC的外接圆的圆心为E，BC中点为H，球心为O，设球半径为r，则由题设条件能够推导出r2=BE2+EO2=
+y2，且r2=
+(
-y)2，由此解得y=1，从而求出r，由此能够求出球的表面积．
| 2 |
| 4 |
| 3 |
| 25 |
| 12 |
| 1 |
| 2 |
解答：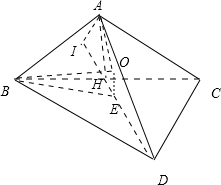
解：由题设知四面体ABCD中，AB=AC=
，BD=DC=CB=2，
如图，设等边△BDC的外接圆的圆心为E，BC中点为H，球心为O，设球半径为r，
则Rt△OEB中，∠OEB=90°，
∵BD=DC=CB=2，AB=AC=
，
∴∠AHE是二面角A-BC-D的平面角，故∠AHE=150°，
DE=
DH=
×
=
，HE=
DH=
，
∴r2=BE2+EO2=
+y2，…①
作AI⊥DH，交DH延长线与I，则AH=1，HE=
，OA=r，∠AHT=180°-∠AHE=30°，
∴AI=
，IE=IH+HE=
+
=
，
∴r2=
+(
-y)2，…②
由①②得y2+
=y2-y+
，解得y=1，
∴r=
=
，
∴球的表面积S=4π(
)2=
．
故选B．
解：由题设知四面体ABCD中，AB=AC=| 2 |
如图，设等边△BDC的外接圆的圆心为E，BC中点为H，球心为O，设球半径为r，
则Rt△OEB中，∠OEB=90°，
∵BD=DC=CB=2，AB=AC=
| 2 |
∴∠AHE是二面角A-BC-D的平面角，故∠AHE=150°，
DE=
| 2 |
| 3 |
| 2 |
| 3 |
| 4-1 |
2
| ||
| 3 |
| 1 |
| 3 |
| ||
| 3 |
∴r2=BE2+EO2=
| 4 |
| 3 |
作AI⊥DH，交DH延长线与I，则AH=1，HE=
| ||
| 3 |
∴AI=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
5
| ||
| 6 |
∴r2=
| 25 |
| 12 |
| 1 |
| 2 |
由①②得y2+
| 4 |
| 3 |
| 7 |
| 3 |
∴r=
|
| ||
| 3 |
∴球的表面积S=4π(
| ||
| 3 |
| 28π |
| 3 |
故选B．
点评：本题考查球的表面积的求法，具体涉及到锥锥的结构特征、二面角的平面角、余弦定理、三角形性质、球的简单性质等知识点，解题时要认真审题，注意合理地化空间几何问题为平面几何问题．
练习册系列答案
相关题目