题目内容
(08年新建二中六模) 如图,等腰直角△![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() .
.
(Ⅰ)求二面角![]() 的正弦值;
的正弦值;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ)证明五点![]() 在同一个球面上,并求
在同一个球面上,并求![]() 两点的球面距离.
两点的球面距离.

解析:方法一
(Ⅰ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,由
,由![]() 知
知![]() ,又
,又![]()
![]() ,故
,故![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理有
 ,
,
所以二面角![]() 的正弦值为
的正弦值为![]()
(Ⅱ)由(Ⅰ)知道![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() ,故
,故![]() 在平面
在平面![]() 上的射影一定在直线
上的射影一定在直线![]() 上,所以点
上,所以点![]() 到平面
到平面![]() 的距离即为△
的距离即为△![]() 的边
的边![]() 上的高.
上的高.
故![]() .
.
(Ⅲ)易证△![]() 为直角三角形,且
为直角三角形,且![]() ,取
,取![]() 的中点
的中点![]() ,则由四边形
,则由四边形![]() 是矩形知
是矩形知![]() ,故五点
,故五点![]() 在以
在以![]() 为球心,
为球心,![]() 为直径的球面上,故
为直径的球面上,故![]() 两点之间的球面距离就是半个大圆的弧长,是
两点之间的球面距离就是半个大圆的弧长,是![]()
方法二
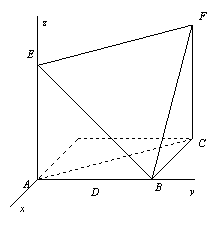
以![]() 点为坐标原点,以过
点为坐标原点,以过![]() 垂直于
垂直于![]() 的直线为
的直线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图所示.
,如图所示.
(Ⅰ)则![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,设
,设![]()
是平面![]() 的法向量,则有
的法向量,则有
 ,即
,即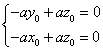 ,取
,取![]() ,
,
得![]() ,易知平面
,易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,故所求角的正弦值为
,故所求角的正弦值为![]() .
.
(Ⅱ)![]() ,故点
,故点![]() 到平面
到平面![]() 的距离为
的距离为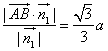 .
.
(Ⅲ)易知![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,故
,故![]() ,
,
而![]() ,故五点
,故五点![]() 在以
在以![]() 为球心,
为球心,![]() 为直径的球面上,故
为直径的球面上,故![]() 两点之间的球面距离就是半个大圆的弧长,是
两点之间的球面距离就是半个大圆的弧长,是![]()


练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
(08年新建二中六模理)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组成.
第一排 | 明文字符 | A | B | C | D |
密码字符 | 11 | 12 | 13 | 14 | |
第二排 | 明文字符 | E | F | G | H |
密码字符 | 21 | 22 | 23 | 24 | |
第三排 | 明文字符 | M | N | P | Q |
密码字符 | 1 | 2 | 3 | 4 |
设随机变量ξ表示密码中不同数字的个数.
(Ⅰ)求P(ξ=2)
(Ⅱ)求随机变量ξ的分布列和它的数学期望.