题目内容
某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是两个全等等腰三角形)根据图中标出的数据,可得这个几何体的表面积为( )


A. | B. | C. | D.12 |
B
试题分析:由已知中的三视图,我们可以得到该几何体是一个底面边长为2,高也为2的正四棱锥,进一步求出四棱锥的侧高,代入棱锥表面积公式,即可求出答案.解:由已知中的三视图我们可得,该几何体是一个底面边长为2,高也为2的正四棱锥,则其侧面的侧高为
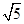 ,则棱锥表面积S=2×2+4×(
,则棱锥表面积S=2×2+4×(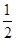 ×2×
×2×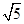 )=4+4
)=4+4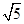 故选B
故选B点评:本题考查的知识点是由三视图求面积,其中根据已知中的三视图,得到该几何体是一个底面边长为2,高也为2的正四棱锥,是解答本题的关键

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
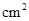




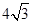 ,则这个圆锥的全面积是( )
,则这个圆锥的全面积是( )

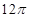

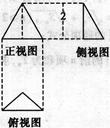
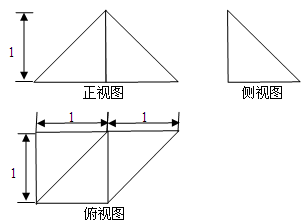



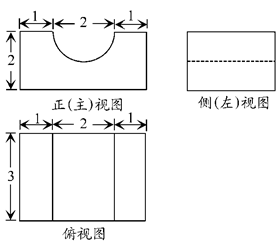
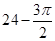
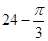
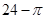
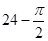
 ,则正视图与侧视图中x的值为( )
,则正视图与侧视图中x的值为( )
 .
.
 .
.
 .
.
 .
.