题目内容
已知圆C1的圆心在坐标原点O,且恰好与直线l1: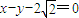 相切.
相切.(Ⅰ)求圆的标准方程;
(Ⅱ)设点A(x,y)为圆上任意一点,AN⊥x轴于N,若动点Q满足
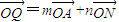 ,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;
,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;(Ⅲ)在(Ⅱ)的结论下,当
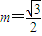 时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.
时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.
【答案】分析:(Ⅰ)根据圆与直线l1: 相切,利用点到直线的距离,求出圆的半径,从而可求圆C1的方程;
相切,利用点到直线的距离,求出圆的半径,从而可求圆C1的方程;
(Ⅱ)设出点的坐标,利用向量条件,确定动点坐标之间的关系,利用A为圆上的点,即可求得动点Q的轨迹方程C2;
(Ⅲ)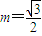 时,曲线C方程为
时,曲线C方程为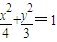 ,假设直线l的方程,与椭圆
,假设直线l的方程,与椭圆 联立,利用韦达定理及向量条件,利用数量积小于0,即可得到结论.
联立,利用韦达定理及向量条件,利用数量积小于0,即可得到结论.
解答:解:(Ⅰ)设圆的半径为r,圆心到直线l1距离为d,则 …(2分)
…(2分)
所以圆C1的方程为x2+y2=4…(3分)
(Ⅱ)设动点Q(x,y),A(x,y),AN⊥x轴于N,N(x,0)
由题意,(x,y)=m(x,y)+n(x,0),所以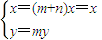 …(5分)
…(5分)
即: ,将
,将 代入x2+y2=4,得
代入x2+y2=4,得 …(7分)
…(7分)
(Ⅲ)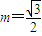 时,曲线C方程为
时,曲线C方程为 ,假设存在直线l与直线l1:
,假设存在直线l与直线l1: 垂直,
垂直,
设直线l的方程为y=-x+b…(8分)
设直线l与椭圆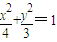 交点B(x1,y1),D(x2,y2)
交点B(x1,y1),D(x2,y2)
联立得: ,得7x2-8bx+4b2-12=0…(9分)
,得7x2-8bx+4b2-12=0…(9分)
因为△=48(7-b2)>0,解得b2<7,且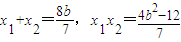 …(10分)
…(10分)
∴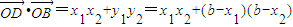 =
=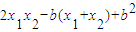
= =
= …(12分)
…(12分)
因为∠BOD为钝角,所以 且b≠0,
且b≠0,
解得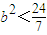 且b≠0,满足b2<7
且b≠0,满足b2<7
∴ 且b≠0,
且b≠0,
所以存在直线l满足题意…(14分)
点评:本题考查圆的标准方程,考查代入法求轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是直线与椭圆方程联立,利用韦达定理进行求解.
 相切,利用点到直线的距离,求出圆的半径,从而可求圆C1的方程;
相切,利用点到直线的距离,求出圆的半径,从而可求圆C1的方程;(Ⅱ)设出点的坐标,利用向量条件,确定动点坐标之间的关系,利用A为圆上的点,即可求得动点Q的轨迹方程C2;
(Ⅲ)
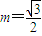 时,曲线C方程为
时,曲线C方程为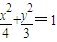 ,假设直线l的方程,与椭圆
,假设直线l的方程,与椭圆 联立,利用韦达定理及向量条件,利用数量积小于0,即可得到结论.
联立,利用韦达定理及向量条件,利用数量积小于0,即可得到结论.解答:解:(Ⅰ)设圆的半径为r,圆心到直线l1距离为d,则
 …(2分)
…(2分)所以圆C1的方程为x2+y2=4…(3分)
(Ⅱ)设动点Q(x,y),A(x,y),AN⊥x轴于N,N(x,0)
由题意,(x,y)=m(x,y)+n(x,0),所以
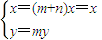 …(5分)
…(5分)即:
 ,将
,将 代入x2+y2=4,得
代入x2+y2=4,得 …(7分)
…(7分)(Ⅲ)
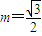 时,曲线C方程为
时,曲线C方程为 ,假设存在直线l与直线l1:
,假设存在直线l与直线l1: 垂直,
垂直,设直线l的方程为y=-x+b…(8分)
设直线l与椭圆
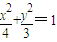 交点B(x1,y1),D(x2,y2)
交点B(x1,y1),D(x2,y2)联立得:
 ,得7x2-8bx+4b2-12=0…(9分)
,得7x2-8bx+4b2-12=0…(9分)因为△=48(7-b2)>0,解得b2<7,且
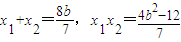 …(10分)
…(10分)∴
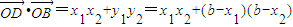 =
=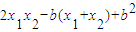
=
 =
= …(12分)
…(12分)因为∠BOD为钝角,所以
 且b≠0,
且b≠0,解得
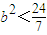 且b≠0,满足b2<7
且b≠0,满足b2<7∴
 且b≠0,
且b≠0,所以存在直线l满足题意…(14分)
点评:本题考查圆的标准方程,考查代入法求轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是直线与椭圆方程联立,利用韦达定理进行求解.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
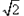 =0相切,
=0相切,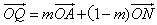 ,(其中m为非零常数),试求动点Q的轨迹方程C2;
,(其中m为非零常数),试求动点Q的轨迹方程C2;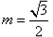 时,得到
时,得到 曲线C,与l1垂直的直线l与曲线C交于B、D两点,求△OBD面积的最大值。
曲线C,与l1垂直的直线l与曲线C交于B、D两点,求△OBD面积的最大值。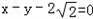 相切.
相切.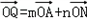 ,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;
,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;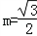 时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.
时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.