题目内容
设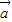 、
、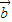 是两个不共线的非零向量 (t∈R)
是两个不共线的非零向量 (t∈R)(1)记
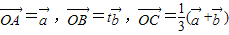 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?(2)若
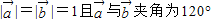 ,那么实数x为何值时
,那么实数x为何值时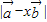 的值最小?
的值最小?
【答案】分析:(1)由三点A,B,C共线,必存在一个常数t使得 ,由此等式建立起关于λ,t的方程求出t的值;
,由此等式建立起关于λ,t的方程求出t的值;
(2)由题设条件,可以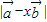 表示成关于实数x的函数,根据所得的函数判断出它取出最小值时的x的值.
表示成关于实数x的函数,根据所得的函数判断出它取出最小值时的x的值.
解答:解:(1)由三点A,B,C共线,必存在一个常数t使得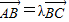 ,则有
,则有
又
∴ =
=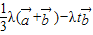 ,又
,又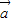 、
、 是两个不共线的非零向量
是两个不共线的非零向量
∴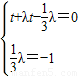 解得
解得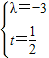
故存在 时,A、B、C三点共线
时,A、B、C三点共线
(2)∵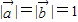 且
且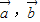 两向量的夹角是120°
两向量的夹角是120°
∴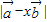 2=
2= =1+x+x2=(x+
=1+x+x2=(x+ )2+
)2+
∴当x=- 时,
时, 的值最小为
的值最小为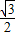
点评:本题考查平面向量的综合题,解题的关键是熟练掌握向量共线的坐标表示,向量的模的坐标表示,理解题设条件,正确转化.本题把三点共线转化为了向量共线,将模的最小值求参数的问题转化为求函数的最小值,解题时要注意恰当地运用转化、化归这一数学思想
 ,由此等式建立起关于λ,t的方程求出t的值;
,由此等式建立起关于λ,t的方程求出t的值;(2)由题设条件,可以
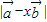 表示成关于实数x的函数,根据所得的函数判断出它取出最小值时的x的值.
表示成关于实数x的函数,根据所得的函数判断出它取出最小值时的x的值.解答:解:(1)由三点A,B,C共线,必存在一个常数t使得
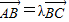 ,则有
,则有
又

∴
 =
=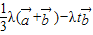 ,又
,又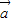 、
、 是两个不共线的非零向量
是两个不共线的非零向量∴
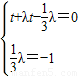 解得
解得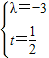
故存在
 时,A、B、C三点共线
时,A、B、C三点共线(2)∵
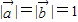 且
且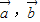 两向量的夹角是120°
两向量的夹角是120°∴
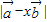 2=
2= =1+x+x2=(x+
=1+x+x2=(x+ )2+
)2+
∴当x=-
 时,
时, 的值最小为
的值最小为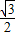
点评:本题考查平面向量的综合题,解题的关键是熟练掌握向量共线的坐标表示,向量的模的坐标表示,理解题设条件,正确转化.本题把三点共线转化为了向量共线,将模的最小值求参数的问题转化为求函数的最小值,解题时要注意恰当地运用转化、化归这一数学思想

练习册系列答案
相关题目
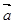 、
、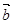 是两个不共线的非零向量(
是两个不共线的非零向量(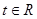 ).
).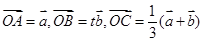 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线? ,那么实数x为何值时
,那么实数x为何值时 的值最小?
的值最小? 、
、 是两个不共线的非零向量 (t∈R)
是两个不共线的非零向量 (t∈R)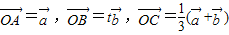 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?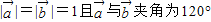 ,那么实数x为何值时
,那么实数x为何值时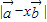 的值最小?
的值最小? ,
,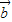 是两个不共线的非零向量,若向量k
是两个不共线的非零向量,若向量k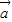 +2
+2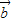 与8
与8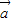 +k
+k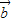 的方向相反,则k= .
的方向相反,则k= . 、
、 是两个不共线的非零向量(
是两个不共线的非零向量(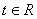 ).
). ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?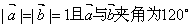 ,那么实数x为何值时
,那么实数x为何值时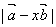 的值最小?
的值最小?