题目内容
设![]() 、
、![]() 是两个不共线的非零向量(t∈R).
是两个不共线的非零向量(t∈R).
(1)记![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,那么当实数
,那么当实数![]() 为何值时,
为何值时,![]() 三点共线?
三点共线?
(2)若![]() =
=![]() =1且
=1且![]() 与
与![]() 夹角为120°,那么实数
夹角为120°,那么实数![]() 为何值时,
为何值时,![]() 的值最小?
的值最小?
(1)∵A、B、C三点共线,∴![]() 与
与![]() 共线,又∵
共线,又∵![]() =
=![]() -
-![]() =tb-a,
=tb-a,![]() =
=![]() -
-![]() =
=![]() b-
b-![]() a,
a,
∴存在实数λ,使![]() =λ
=λ![]() ,
,
即tb-a=![]() b-
b-![]() a,∴t=
a,∴t=![]() .
.
(2)∵|a|=|b|=1,〈a,b〉=120°,∴a·b=-![]() ,
,
∴|a+xb|2=|a|2+x2|b|2-2x·a·b=1+x2+x
=(x-![]() )2+
)2+![]() ≥
≥![]() ,
,
∴|a-xb|的最小值为![]() ,此时x=
,此时x=![]() .
.

练习册系列答案
相关题目
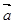 、
、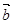 是两个不共线的非零向量(
是两个不共线的非零向量(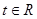 ).
).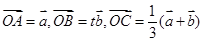 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线? ,那么实数x为何值时
,那么实数x为何值时 的值最小?
的值最小?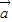 、
、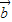 是两个不共线的非零向量 (t∈R)
是两个不共线的非零向量 (t∈R)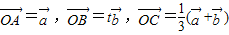 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?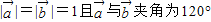 ,那么实数x为何值时
,那么实数x为何值时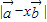 的值最小?
的值最小? ,
,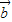 是两个不共线的非零向量,若向量k
是两个不共线的非零向量,若向量k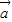 +2
+2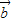 与8
与8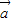 +k
+k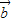 的方向相反,则k= .
的方向相反,则k= . 、
、 是两个不共线的非零向量(
是两个不共线的非零向量(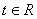 ).
). ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?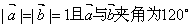 ,那么实数x为何值时
,那么实数x为何值时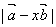 的值最小?
的值最小?