题目内容
若一元二次方程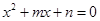 中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )
中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )
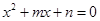 中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )
中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )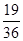
解:连续抛掷两次骰子分别得到的点数记作(m,n):
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).共36个
若要使一元二次方程x2+mx+n=0有实根,则m2-4n≥0,则满足条件的情况有
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(4,4),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).共19种
故程有实根的概率P="19" /36
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).共36个
若要使一元二次方程x2+mx+n=0有实根,则m2-4n≥0,则满足条件的情况有
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(4,4),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).共19种
故程有实根的概率P="19" /36

练习册系列答案
相关题目
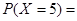 ___________.
___________. 通晓日语,
通晓日语,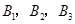 通晓俄语,
通晓俄语, 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组. 被选中的概率;
被选中的概率;  和
和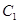 不全被选中的概率.
不全被选中的概率.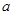 ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为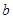 ,且
,且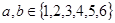 ,若
,若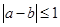 ,则称“甲乙心有灵犀”, 现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.
,则称“甲乙心有灵犀”, 现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.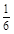 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。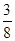

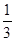
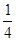
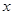 的二次函数
的二次函数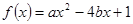 ,
,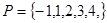 ,和
,和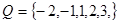 分别从集合
分别从集合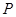 和
和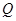 中随机取出一个数作为
中随机取出一个数作为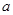 和
和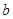 ,求函数
,求函数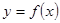 在区间
在区间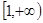 上是增函数的概率;
上是增函数的概率;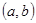 是区域
是区域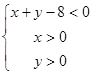
 的随机点,求函数
的随机点,求函数