题目内容
国家射击队的队员为在2010年亚运会上取得优异成绩,正在加紧备战,经过近期训练,某队员射击一次,命中7~10环的概率如下表所示:
求该射击队员射击一次
(1)射中9环或10环的概率;
(2)至少命中8环的概率;
(3)命中不足8环的概率.
| 命中环数 | 10环 | 9环 | 8环 | 7环 |
| 概率 | 0.32 | 0.28 | 0.18 | 0.12 |
(1)射中9环或10环的概率;
(2)至少命中8环的概率;
(3)命中不足8环的概率.
(1)0.60;(2)0.78;(3)0.22.
(1)事件“射击一次,命中k环”为Ak(k∈N,k≤10),则事件Ak彼此互斥,然后根据互斥事件的概率计算方法求和即可。
(2)“射击一次,至少命中8环”包括命中8环,9环,10环三个事件。这三个事件是互斥的,然后根据互斥事件的概率计算方法求和即可。
(3) “射击一次,命中不足8环”是事件B:“射击一次,至少命中8环”的对立事件,
根据对立事件的概率公式P(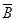 )=1-P(B)计算即可.
)=1-P(B)计算即可.
解:记事件“射击一次,命中k环”为Ak(k∈N,k≤10),则事件Ak彼此互斥.
(1)记“射击一次,射中9环或10环”为事件A,那么当A9,A10之一发生时,事件A发生,由互斥事件的概率加法公式得
P(A)=P(A9)+P(A10)=0.32+0.28=0.60.
(2)设“射击一次,至少命中8环”的事件为B,那么当A8,A9,A10之一发生时,事件B发生.
由互斥事件的概率加法公式得
P(B)=P(A8)+P(A9)+P(A10)
=0.18+0.28+0.32=0.78.
(3)由于事件“射击一次,命中不足8环”是事件B:“射击一次,至少命中8环”的对立事件,即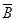 表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得
表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得
P(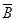 )=1-P(B)=1-0.78=0.22.
)=1-P(B)=1-0.78=0.22.
(2)“射击一次,至少命中8环”包括命中8环,9环,10环三个事件。这三个事件是互斥的,然后根据互斥事件的概率计算方法求和即可。
(3) “射击一次,命中不足8环”是事件B:“射击一次,至少命中8环”的对立事件,
根据对立事件的概率公式P(
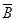 )=1-P(B)计算即可.
)=1-P(B)计算即可.解:记事件“射击一次,命中k环”为Ak(k∈N,k≤10),则事件Ak彼此互斥.
(1)记“射击一次,射中9环或10环”为事件A,那么当A9,A10之一发生时,事件A发生,由互斥事件的概率加法公式得
P(A)=P(A9)+P(A10)=0.32+0.28=0.60.
(2)设“射击一次,至少命中8环”的事件为B,那么当A8,A9,A10之一发生时,事件B发生.
由互斥事件的概率加法公式得
P(B)=P(A8)+P(A9)+P(A10)
=0.18+0.28+0.32=0.78.
(3)由于事件“射击一次,命中不足8环”是事件B:“射击一次,至少命中8环”的对立事件,即
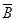 表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得
表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得P(
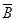 )=1-P(B)=1-0.78=0.22.
)=1-P(B)=1-0.78=0.22.
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
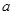 ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为
,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为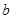 .求关于
.求关于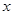 的一元二次方程
的一元二次方程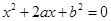 有实根的概率;
有实根的概率; 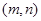 作为点P的坐标,求点P落在区域
作为点P的坐标,求点P落在区域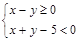 内的概率.
内的概率.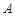 往
往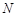 走,且只能向右或向下走,随机地选一种走法,则经过点
走,且只能向右或向下走,随机地选一种走法,则经过点 的概率是 .
的概率是 .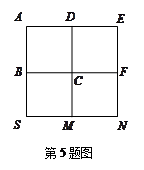
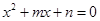 中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )
中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )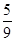
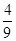


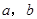 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“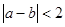 ”,其中
”,其中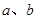 为实常数.
为实常数.