题目内容
已知函数 。
。
(1)若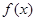 的单调增区间是(0,1)求m的值。
的单调增区间是(0,1)求m的值。
(2)当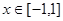 时,函数
时,函数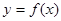 的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
【答案】
(1) ;(2)由
;(2)由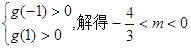 。
。
【解析】
试题分析:(1)先求出导函数f'(x),根据函数f(x)在区间(0, 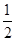 )上单调递增,在区间(
)上单调递增,在区间( 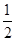 ,1)上单调递减,可知x=
,1)上单调递减,可知x=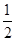 是函数的极值,从而f'(
是函数的极值,从而f'(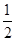 )=0,解之即可求出m的值;
)=0,解之即可求出m的值;
(2)本小问可转化成f'(x)=3mx2-6(m+1)x+3m+6>3m在区间[-1,1]恒成立,即3mx2-6(m+1)x+6>0在区间[-1,1]恒成立,将x=-1和x=1代入使之成立,即可求出m的范围
(1)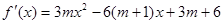

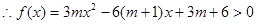 的解集为(0,1),
的解集为(0,1),
则0,1是关于x的方程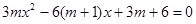 的两根
的两根
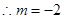
(2)由已知,当
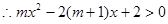
又m<0,要使 上恒成立
上恒成立
只需满足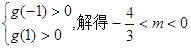
考点:本题主要考查了函数恒成立问题,以及利用导数研究函数的单调性等基础知识,考查计算能力和分析问题的能力,属于基础题.
点评:解决该试题的关键是利用导数得到函数的单调去甲,以及函数的极值,进而得到从那数m的值,同时对于恒成立问题的转化思想的运用,求解最值得到参数的范围。

练习册系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为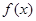 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素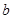 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程