题目内容
已知抛物线C的顶点在坐标原点,焦点在x轴的正半轴,且焦点到准线的距离为2,直线l与抛物线C相交于A,B两点,若M(2,2)满足
=
,求直线l的方程.
| AM |
| MB |
分析:设抛物线方程为y2=2px(p>0),易求抛物线方程为y2=4x,由
=
知M为线段AB的中点,设A(x1,y1),B(x2,y2),联立方程
,可得k2x2+[4k(1-k)-4]x+4(1-k)2=0,利用韦达定理列关系式可求得k.
| AM |
| MB |
|
解答:解:设抛物线方程为y2=2px(p>0),则p=2,抛物线方程为y2=4x.
由
=
知M为线段AB的中点.
设A(x1,y1),B(x2,y2),
当直线斜率不存在时不满足题意.
∴设直线l的方程为:y-2=k(x-2),
联立
消y得k2x2+[4k(1-k)-4]x+4(1-k)2=0,
则
=
=2,
解得k=1,
∴直线l的方程为:x-y=0.
由
| AM |
| MB |
设A(x1,y1),B(x2,y2),
当直线斜率不存在时不满足题意.
∴设直线l的方程为:y-2=k(x-2),
联立
|
则
| x1+x2 |
| 2 |
| 4k2-4k+4 |
| 2k2 |
解得k=1,
∴直线l的方程为:x-y=0.
点评:本题考查抛物线的简单性质,考查直线与圆锥曲线的位置关系,突出考查方程思想与运算能力,属于中档题.

练习册系列答案
相关题目
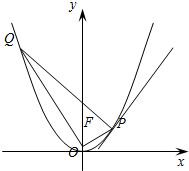 已知抛物线C的顶点在原点,焦点为F(0,1).
已知抛物线C的顶点在原点,焦点为F(0,1).