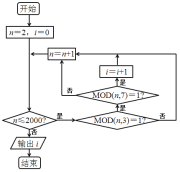
题目内容
【题目】已知椭圆![]() 的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且
的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且![]() 的面积为1.
的面积为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上位于第一象限内一动点,直线![]() 与
与![]() 轴交于点C,直线
轴交于点C,直线![]() 与
与![]() 轴交于点D,求证:四边形
轴交于点D,求证:四边形![]() 的面积为定值.
的面积为定值.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)由长轴长是短轴长的2倍,![]() 的面积,构建方程组,求得ab,代入椭圆方程得答案;
的面积,构建方程组,求得ab,代入椭圆方程得答案;
(2)设![]() 有
有![]() ,分别表示直线
,分别表示直线![]() 和
和![]() 的方程,从而表示
的方程,从而表示![]() 与
与![]() ,可得
,可得![]() 与
与![]() 长度关系式,进而可以表示
长度关系式,进而可以表示![]() ,化简即证..
,化简即证..
(1)∵椭圆![]() 的长轴长是短轴长的2倍,∴
的长轴长是短轴长的2倍,∴![]() .
.
∵![]() 的面积为1,∴
的面积为1,∴![]() ,
,![]() ,
,
解得![]() ,
,![]() .
.
∴椭圆C的方程为![]() .
.
(2)由(1)可知![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,即
,即![]() .
.
则直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() ,即
,即![]() .
.
同理,直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() .
.
∴![]()
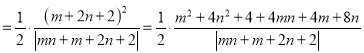
因为![]() 且
且![]() ,
,
则原式![]() .
.
∴四边形![]() 的面积为定值2.
的面积为定值2.

 阅读快车系列答案
阅读快车系列答案【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率作了调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如表:
个人所得税税率表 | 个人所得税税率表 | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率 | 级数 | 全月应纳税所得额 | 税率 |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
|
|
|
|
|
|
(1)假如小明某月的工资、薪金等税前收入为7500元,请你帮小明算一下调整后小明的实际收入比调整前增加了多少?
(2)某税务部门在小明所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入 |
|
|
|
|
|
|
人数 | 40 | 30 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量X表示抽到作为宣讲员的收入在
的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量X表示抽到作为宣讲员的收入在![]() 元的人数,求X的分布列与数学期望.
元的人数,求X的分布列与数学期望.
【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表周数
周数x | 6 | 5 | 4 | 3 | 2 | 1. |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
其中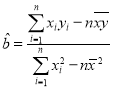 ,
,![]() ,
,![]() ,
,![]()
(1)作出散点图;
(2)根据上表数据用最小二乘法求出y关于x的线性回方程![]() (精确到0.01)
(精确到0.01)
(3)根据经验观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及以上为重度焦虑。若为中度焦虑及以上,则要进行心理疏导。若一个学生在距高考第二周时观测值为103,则该学生是否需要进行心理疏导?