题目内容
【题目】已知函数![]() .
.
(1)判断函数![]() 的单调性;
的单调性;
(2)若对任意![]() 时,都有
时,都有![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 为常量函数,不存在单调性;当
为常量函数,不存在单调性;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】
(1)要判断函数![]() 的单调性,需求导数,对
的单调性,需求导数,对![]() 进行讨论;
进行讨论;
(2)由![]() ,得
,得![]() , 令
, 令![]() ,计算
,计算![]() ,然后分
,然后分![]() ,
,![]() ,
,![]() 三种情况讨论即可.
三种情况讨论即可.
解:(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,令
时,令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() ,
,
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 为常量函数,不存在单调性;
为常量函数,不存在单调性;
当![]() 时,令
时,令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() ,
,
故函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)由![]() ,
,
得![]() ,
,
得![]() ,
,
得![]() ,
,
得![]() ,
,
令![]() ,
,
则![]() .
.
由题意知,![]() ,则有
,则有![]() ,所以
,所以![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
而![]() ,不满足
,不满足![]() ;
;
②若![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
由题意得![]() ,
,
解得![]() ,所以
,所以![]() ;
;
③若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
故![]() 时,
时,![]() 恒成立.
恒成立.
综上,实数a的取值范围是![]()

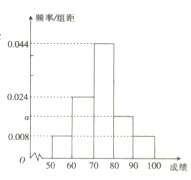
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活.一媒体为调查市民对低头族的认识,从某社区的500名市民中随机抽取n名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
组数 | 分组(单位:岁) | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 20 | 0.20 |
3 |
| a | 0.35 |
4 |
| 30 | b |
5 |
| 10 | 0.10 |
合计 | n | 1.00 | |
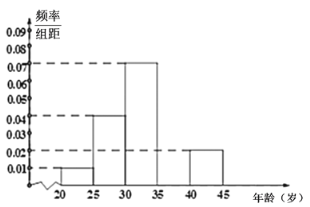
(1)求出表中a,b,n的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定在第2,4,5组中用分层抽样的方法抽取6名市民进行问卷调查,再从这6名1民中随机抽取2名接受电视采访,求第2组至少有一名接受电视采访的概率.
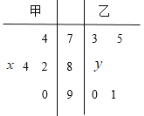
【题目】某校医务室欲研究昼夜温差大小与高三患感冒人数多少之间的关系,他们统计了2019年9月至2020年1月每月8号的昼夜温差情况与高三因患感冒而就诊的人数,得到如下资料:
日期 | 2019年9月8日 | 2019年10月8日 | 2019年11月8日 | 2019年12月8日 | 2020年1月8日 |
昼夜温差 | 5 | 8 | 12 | 13 | 16 |
就诊人数 | 10 | 16 | 26 | 30 | 35 |
该医务室确定的研究方案是先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.假设选取的是2019年9月8日与2020年1月8日的2组数据.
(1)求就诊人数![]() 关于昼夜温差
关于昼夜温差![]() 的线性回归方程
的线性回归方程![]() (结果精确到0.01)
(结果精确到0.01)
(2)若由(1)中所求的线性回归方程得到的估计数据与所选出的检验数据的误差均不超过3人,则认为得到的线性回归方程是理想的,试问该医务室所得线性回归方程是否理想?
参考公式: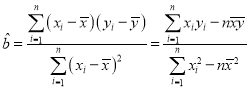 ,
,![]() .
.