题目内容
17.设f(n)=1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$(n∈N*),计算的f(2)=$\frac{3}{2}$,f(4)>2,f(8)>$\frac{5}{2}$,f(16)>3,…,观察上述结果,按照上面规律,可以推测f(2048)>$\frac{13}{2}$.分析 把已知的式子进行转化,然后寻找相应的规律.
解答 解:由已知中:
f(2)=$\frac{3}{2}$,
f(4)>2,
f(8)>$\frac{5}{2}$,
f(16)>3,
…,
归纳可得:
f(2n)>$\frac{n+2}{2}$,
∵2048=211,
故f(2048)>$\frac{13}{2}$,
故答案为:$\frac{13}{2}$
点评 本题考查归纳推理,把已知的式子变形找规律是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知复数z满足z•i=2-i,i为虚数单位,则z的共轭复数$\overline{z}$等于( )
| A. | 2-i | B. | -1+2i | C. | 1+2i | D. | -1-2i |
12.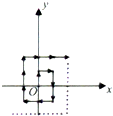 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |
