题目内容
已知α,β均为锐角,sinα=
,cosβ=
,求α-β的值.
| ||
| 5 |
| ||
| 10 |
分析:依题意,通过求sin(α-β)可求得α-β的值.
解答:解:由已知得:cosα=
=
,sinβ=
=
,
∵sinα<sinβ且α,β均为锐角,
∴0<α<β<
,
∴-
<α-β<0,
又sin(α-β)=sinαcosβ-cosαsinβ=-
,
∴α-β=-
.
| 1-sin2α |
2
| ||
| 5 |
| 1-cos2β |
3
| ||
| 10 |
∵sinα<sinβ且α,β均为锐角,
∴0<α<β<
| π |
| 2 |
∴-
| π |
| 2 |
又sin(α-β)=sinαcosβ-cosαsinβ=-
| ||
| 2 |
∴α-β=-
| π |
| 4 |
点评:本题考查两角和与差的正弦函数,考查同角三角函数间的基本关系,求得sin(α-β)是关键,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
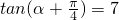 ,
, ,α,β均为锐角.
,α,β均为锐角.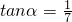 ,
,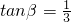 ,α,β均为锐角
,α,β均为锐角 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 ,设
,设 ,
, 均为锐角.
均为锐角. ;
; 的数量积
的数量积 的值.
的值.