题目内容
(本小题共14分)
已知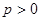 ,动点
,动点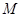 到定点
到定点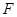
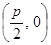 的距离比
的距离比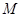 到定直线
到定直线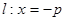 的距离小
的距离小 .
.
(I)求动点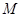 的轨迹
的轨迹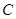 的方程;
的方程;
(Ⅱ)设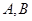 是轨迹
是轨迹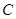 上异于原点
上异于原点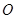 的两个不同点,
的两个不同点,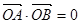 ,求
,求 面积的最小值;
面积的最小值;
(Ⅲ)在轨迹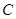 上是否存在两点
上是否存在两点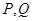 关于直线
关于直线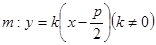 对称?若存在,求出直线
对称?若存在,求出直线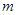 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
【答案】
(1)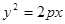 (2)
(2)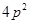 (3)不存在
(3)不存在
【解析】(Ⅰ)∵动点 到定点
到定点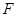 与到定直线
与到定直线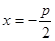 的距离相等
的距离相等
∴点 的轨迹为抛物线,轨迹
的轨迹为抛物线,轨迹 的方程为:
的方程为: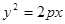 . ……………4分
. ……………4分
(Ⅱ)设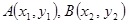
∵
∴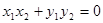 [来源:Z,xx,k.Com]
[来源:Z,xx,k.Com]
∵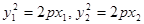
∴
∴
=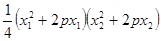
=

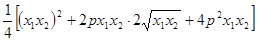 =
=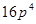
∴当且仅当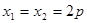 时取等号,
时取等号, 面积最小值为
面积最小值为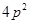 . ……………9分
. ……………9分
(Ⅲ)设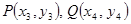 关于直线
关于直线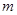 对称,且
对称,且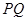 中点
中点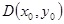
∵ 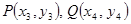 在轨迹
在轨迹 上
上
∴
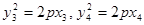
两式相减得: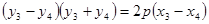
∴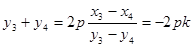
∴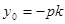
∵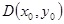 在
在 上
上
∴ ,点
,点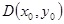 在抛物线外
在抛物线外
∴在轨迹 上不存在两点
上不存在两点 关于直线
关于直线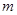 对称.
……………14分
对称.
……………14分

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是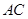 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.