题目内容
【题目】已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q>0,n∈N* .
(1)若2a2 , a3 , a2+2成等差数列,求an的通项公式;
(2)设双曲线x2﹣ ![]() =1的离心率为en , 且e2=
=1的离心率为en , 且e2= ![]() ,证明:e1+e2++en>
,证明:e1+e2++en> ![]() .
.
【答案】
(1)
解:∵Sn+1=qSn+1 ①,∴当n≥2时,Sn=qSn﹣1+1 ②,两式相加你可得an+1=qan,
即从第二项开始,数列{an}为等比数列,公比为q.
当n=1时,∵数列{an}的首项为1,∴a1+a2=S2=qa1+1,∴a2=q=a1q,
∴数列{an}为等比数列,公比为q.
∵2a2,a3,a2+2成等差数列,
∴2q+q+2=2q2,求得q=2,或 q=﹣ ![]() .
.
根据q>0,故取q=2,∴an=2n﹣1,n∈N*
(2)
证明:设双曲线x2﹣ ![]() =1的离心率为en,
=1的离心率为en,
∴en= ![]() =
= ![]() .
.
由于数列{an}为首项等于1、公比为q的等比数列,
∴e2= ![]() =
= ![]() =
= ![]() ,q=
,q= ![]() ,
,
∴an= ![]() ,∴en=
,∴en= ![]() =
= ![]() >
> ![]() =
= ![]() .
.
∴e1+e2++en>1+ ![]() +
+ ![]() +…+
+…+ ![]() =
= 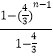 =
= ![]() ,原不等式得证
,原不等式得证
【解析】(1)由条件利用等比数列的定义和性质,求得数列{an}为首项等于1、公比为q的等比数列,再根据2a2 , a3 , a2+2成等差数列求得公比q的值,可得{an}的通项公式.
(2)利用双曲线的定义和简单性质求得en=![]() ,根据e2=
,根据e2= ![]() =
= ![]() ,求得q的值,可得{aspan>n}的解析式,再利用放缩法可得∴en=
,求得q的值,可得{aspan>n}的解析式,再利用放缩法可得∴en= ![]() >
>![]() ,从而证得不等式成立.
,从而证得不等式成立.
本题主要考查等差数列、等比数列的定义和性质,用放缩法进行数列求和,数曲线的简单性质,属于难题.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系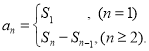 .
.

【题目】下表是高三某位文科生连续5次月考的历史、政治的成绩,结果统计如下:
月份 | 9 | 10 | 11 | 12 | 1 |
历史(x分) | 79 | 81 | 83 | 85 | 87 |
政治(y分) | 77 | 79 | 79 | 82 | 83 |
(1)求该生5次月考历史成绩的平均分和政治成绩的方差
(2)一般来说,学生的历史成绩与政治成绩有较强的线性相关,根据上表提供的数据,求两个变量x、y的线性回归方程 ![]() =
= ![]() x+
x+ ![]()
(附: ![]() =
=  =
=  ,
, ![]() =y﹣
=y﹣ ![]() x)
x)
