Question

【题目】如图（1）.在中，，，，、分别是、上的点，且，将沿折起到的位置，使，如图（2）.

（1）求证：平面；

（2）当点在何处时，三棱锥体积最大，并求出最大值；

（3）当三棱锥体积最大时，求与平面所成角的大小.

Answer 1

【答案】（1）见解析（2）点位于中点时，三棱锥体积最大，最大值为（3）

【解析】

(1)根据线面垂直的判定定理证明；

(2)将三棱锥的体积表示成某个变量的函数，再求其最大值；

(3)先找出线面角的平面角，再解三角形求角.

（1）证明：∵，，

∴，因此，

所以，

又∵，

∴平面；

（2）解：设，则，

由（1），又因为，，

∴平面；

所以，

因此当，即点位于中点时，

三棱锥体积最大，最大值为；

（3）解：如图，联结，

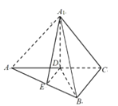
由于，且，

∴，即，

因此即为与平面所成角，

∵，

∴，

所以，

即与平面所成角的大小为.