题目内容
在正四面体ABCD中,E、F分别是BC、AD中点,则异面直线AE与CF所成的角是分析:连接ED,取ED的中点M,连接CM、FM,则FM∥AE,且FM=
AE,所以异面直线AE与CF所成的角即为∠CFM或其补角,然后在Rt△MEC中,借助正弦或余弦定理解出所求的角.
| 1 |
| 2 |
解答: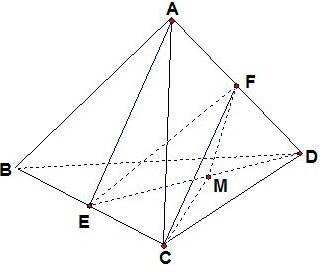 解:如图所示:设正四面体ABCD的棱长为a,
解:如图所示:设正四面体ABCD的棱长为a,
连接ED,取ED的中点M,连接CM、FM,则FM∥AE,且FM=
AE,
∴异面直线AE与CF所成的角即为∠CFM或其补角,
∵AE=CF=
a,
∴FM=
a
在Rt△MEC中,EC=
a,EM=
a,
∴MC=
a
∴cos∠CFM=
=
∴∠CFM=arccos
.
故选Arccos
 解:如图所示:设正四面体ABCD的棱长为a,
解:如图所示:设正四面体ABCD的棱长为a,连接ED,取ED的中点M,连接CM、FM,则FM∥AE,且FM=
| 1 |
| 2 |
∴异面直线AE与CF所成的角即为∠CFM或其补角,
∵AE=CF=
| ||
| 2 |
∴FM=
| ||
| 4 |
在Rt△MEC中,EC=
| 1 |
| 2 |
| ||
| 4 |
∴MC=
| ||
| 4 |
∴cos∠CFM=
| CF2+FM2-MC2 |
| 2CF•FM |
| 2 |
| 3 |
∴∠CFM=arccos
| 2 |
| 3 |
故选Arccos
| 2 |
| 3 |
点评:本题主要考查了异面直线所成的角,空间中的线面关系,解三角形等基础知识,考查空间想象能力和思维能力.求异面直线所成的角,一般有两种方法,一种是几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.还有一种方法是向量法,即建立空间直角坐标系,利用向量的代数法和几何法求解.

练习册系列答案
相关题目