题目内容
已知有关正三角形的一个结论：“在正三角形ABC中，若D是BC的中点，G是三角形ABC内切圆的圆心，则
=2”．若把该结论推广到正四面体（所有棱长均相等的三棱锥），则有结论：“在正四面体ABCD中，若M是正三角形BCD的中心，O是在正四面体ABCD内切球的球心，则
=
| AG |
| GD |
| AO |
| OM |
3
3
”．分析：类比平面几何结论，推广到空间，则有结论：“
=3”．设正四面体ABCD边长为1，易求得AM=
，又O到四面体各面的距离都相等，所以O为四面体的内切球的球心，设内切球半径为r，则有r=
，可求得r即OM，从而可验证结果的正确性．
| AO |
| OM |
| ||
| 3 |
| 3V |
| S表 |
解答：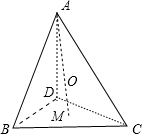
解：推广到空间，则有结论：“
=3”．
设正四面体ABCD边长为1，易求得AM=
，又O到四面体各面的距离都相等，
所以O为四面体的内切球的球心，设内切球半径为r，
则有r=
，可求得r即OM=
，
所以AO=AM-OM=
，所以
=3．
故答案为：3
解：推广到空间，则有结论：“| AO |
| OM |
设正四面体ABCD边长为1，易求得AM=
| ||
| 3 |
所以O为四面体的内切球的球心，设内切球半径为r，
则有r=
| 3V |
| S表 |
| ||
| 12 |
所以AO=AM-OM=
| ||
| 4 |
| AO |
| OM |
故答案为：3
点评：本题考查类比推理、几何体的结构特征、体积法等基础知识，考查运算求解能力，考查空间想象力、化归与转化思想．属于基础题．
练习册系列答案
相关题目
=2”．若把该结论推广到正四面体（所有棱长均相等的三棱锥），则有结论：“在正四面体ABCD中，若M是正三角形BCD的中心，O是在正四面体ABCD内切球的球心，则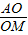
= ”．