题目内容
①求平行于直线3x+4y-12=0,且与它的距离是7的直线的方程;
②求垂直于直线x+3y-5="0,"
且与点P(-1,0)的距离是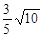 的直线的方程.
的直线的方程.
【答案】
(1)3x+4y+23=0或3x+4y-47=0;(2)3x-y+9=0或3x-y-3=0.
【解析】
试题分析:(1)由题意设所求直线的方程为3x+4y+m=0,
则直线的距离d=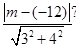 =7,
=7,
化简得|12+m|=35,即12+m=35,12+m=-35,解得m=23,m=-47;
则所求直线的方程为3x+4y+23=0或3x+4y-47=0;
(2)由所求的直线与直线x+3y-5=0垂直,可设所求的直线方程为 3x-y+k=0,
再由点P(-1,0)到它的距离为
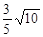 =
=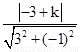 ,所以,|k-3|=6,解得k=9,-3;
,所以,|k-3|=6,解得k=9,-3;
故所求的直线方程为 3x-y+9=0或3x-y-3=0.
考点:直线方程,点到直线的距离。
点评:中档题,确定直线的方程,常用方法是“待定系数法”。利用已知条件,灵活假设方程的形式,利用点到直线的距离公式,建立方程求解待定系。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
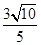 的直线方程.
的直线方程.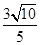 的直线方程.
的直线方程.