题目内容
①求平行于直线3x+4y-12=0,且与它的距离是7的直线的方程;
②求垂直于直线x+3y-5=0,且与点P(-1,0)的距离是
的直线的方程.
②求垂直于直线x+3y-5=0,且与点P(-1,0)的距离是
| 3 |
| 5 |
| 10 |
分析:①由所求的直线与直线l平行设出所求直线的方程为3x+4y+m=0,根据平行线间的距离公式列出关于m的方程,求出方程的解得到m的值,写出所求的直线方程即可.
②根据两直线垂直,设所求的直线方程为 x-2y+k=0,再根据点P(2,1)到它的距离列方程求出k的值,即得所求的直线方程.
②根据两直线垂直,设所求的直线方程为 x-2y+k=0,再根据点P(2,1)到它的距离列方程求出k的值,即得所求的直线方程.
解答:解:①由题意设所求直线的方程为3x+4y+m=0,
则直线的距离d=
=7,
化简得|12+m|=35,即12+m=35,12+m=-35,
解得m=23,m=-47;
则所求直线的方程为3x+4y+23=0或3x+4y-47=0;
②由所求的直线与直线x+3y-5=0垂直,可设所求的直线方程为 3x-y+k=0,
再由点P(-1,0)到它的距离为
=
⇒|k-3|=6;
解得k=9,-3;
故所求的直线方程为 3x-y+9=0或3x-y-3=0.
则直线的距离d=
| |m-(-12)| | ||
|
化简得|12+m|=35,即12+m=35,12+m=-35,
解得m=23,m=-47;
则所求直线的方程为3x+4y+23=0或3x+4y-47=0;
②由所求的直线与直线x+3y-5=0垂直,可设所求的直线方程为 3x-y+k=0,
再由点P(-1,0)到它的距离为
| 3 |
| 5 |
| 10 |
| |-3+k| | ||
|
解得k=9,-3;
故所求的直线方程为 3x-y+9=0或3x-y-3=0.
点评:此题考查学生掌握两直线平行以及垂直时直线方程的关系,灵活运用两条平行直线间的距离公式化简求值,是一道中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
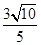 的直线方程.
的直线方程.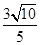 的直线方程.
的直线方程.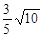 的直线的方程.
的直线的方程.