Question

解答下列问题：

（1）求平行于直线3x+4y 2=0,且与它的距离是1的直线方程；

（2）求垂直于直线x+3y 5=0且与点P( 1,0)的距离是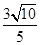的直线方程.

 

Answer 1

【答案】

（1）3x+4y+3=0或3x+4y 7=0 (2) 3x y+9=0或3x y 3=0 

【解析】

试题分析：（1）将平行线的距离转化为点到线的距离，用点到直线的距离公式求解；（2）由相互垂直设出所求直线方程，然后由点到直线的距离求解.

试题解析：解：（1）设所求直线上任意一点P（x，y），由题意可得点P到直线的距离等于1，即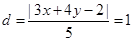，∴3x+4y 2=±5，即3x+4y+3=0或3x+4y 7=0．

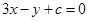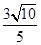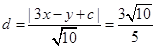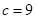（2）所求直线方程为，由题意可得点P到直线的距离等于，即，∴或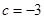，即3x y+9=0或3x y 3=0．

考点：1.两条平行直线间的距离公式；2.两直线的平行与垂直关系