题目内容
设函数 是定义在
是定义在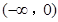 上的可导函数,其导函数为
上的可导函数,其导函数为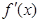 ,且有
,且有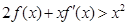 ,则不等式
,则不等式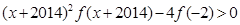 的解集为( )
的解集为( )
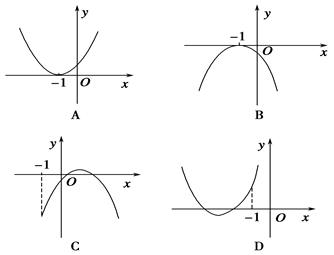
A.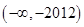 | B.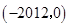 | C.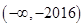 | D.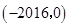 |

解析试题分析:由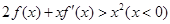 可得
可得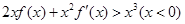 即
即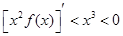
令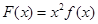 则当
则当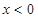 时,有
时,有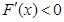 ,即
,即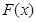 在
在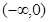 上单调递减.所以
上单调递减.所以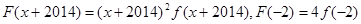 .即不等式等价为
.即不等式等价为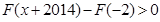
因为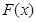 在
在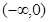 上单调递减所以由
上单调递减所以由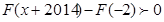 ,即
,即 得
得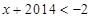 ,解得
,解得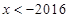
考点:函数单调性和导数之间的关系,利用条件构造函数,解不等式.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
函数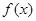 在定义域R内可导,若
在定义域R内可导,若
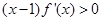 ,若
,若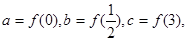 则
则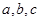 的大小关系是( )
的大小关系是( )
A.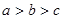 | B.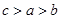 | C.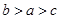 | D.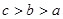 |
设函数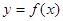 在
在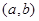 上的导函数为
上的导函数为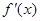 ,
,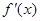 在
在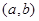 上的导函数为
上的导函数为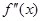 ,若在
,若在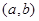 上,
上,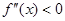 恒成立,则称函数
恒成立,则称函数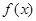 在
在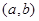 上为“凸函数”.已知当
上为“凸函数”.已知当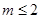 时,
时,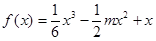 在
在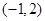 上是“凸函数”.则
上是“凸函数”.则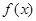 在
在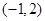 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
过曲线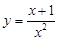 (
( )上横坐标为1的点的切线方程为( )
)上横坐标为1的点的切线方程为( )
A. | B.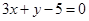 |
C.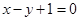 | D. |
函数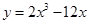 在区间
在区间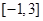 上的最大值和最小值分别为( )
上的最大值和最小值分别为( )
A.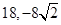 | B.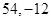 | C.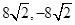 | D.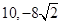 |
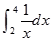 等于( )
等于( )
A. | B.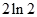 | C.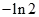 | D. |
曲线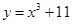 在点
在点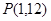 处的切线与
处的切线与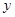 轴交点的纵坐标是( )
轴交点的纵坐标是( )
| A.-9 | B.-3 | C.9 | D.15 |
下列关于函数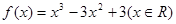 的性质叙述错误的是( )
的性质叙述错误的是( )
A. 在区间 在区间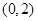 上单调递减 上单调递减 |
B. 在定义域上没有最大值 在定义域上没有最大值 |
C. 在 在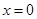 处取最大值3 处取最大值3 |
D. 的图像在点 的图像在点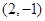 处的切线方程为 处的切线方程为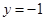 |