题目内容
设函数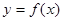 在
在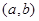 上的导函数为
上的导函数为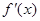 ,
,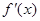 在
在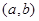 上的导函数为
上的导函数为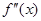 ,若在
,若在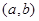 上,
上,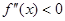 恒成立,则称函数
恒成立,则称函数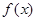 在
在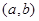 上为“凸函数”.已知当
上为“凸函数”.已知当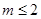 时,
时,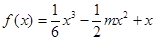 在
在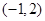 上是“凸函数”.则
上是“凸函数”.则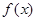 在
在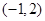 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
C
解析试题分析:由题设可知: 在(-1,2)上恒成立,由于
在(-1,2)上恒成立,由于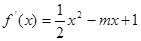 从而
从而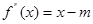 ,所以有
,所以有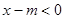 在(-1,2)上恒成立,故知
在(-1,2)上恒成立,故知 ,又因为
,又因为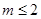 ,所以
,所以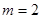 ;从而
;从而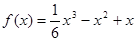 ,
,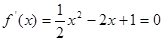 得
得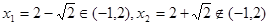 ;且当
;且当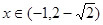 时
时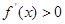 ,当
,当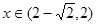 时
时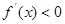 ,所以
,所以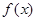 在
在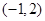 上在
上在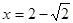 处取得极大值,没有极小值.
处取得极大值,没有极小值.
考点:新定义,函数的极值.

练习册系列答案
相关题目
抛物线 在点
在点 处的切线的倾斜角是( )
处的切线的倾斜角是( )
A.30 | B.45 | C.60 | D.90 |
点P是曲线x2-y-2ln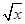 =0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
=0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
A.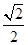 (1-ln 2) (1-ln 2) | B.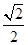 (1+ln 2) (1+ln 2) | C.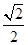 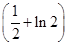 | D.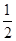 (1+ln 2) (1+ln 2) |
已知函数 的导函数为
的导函数为 ,若
,若 时,
时,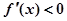 ;
; ;
;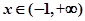 时,
时,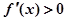 ,则
,则 ( )
( )
| A.25 | B.17 | C. | D.1 |
已知函数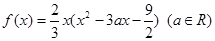 ,若函数
,若函数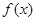 的图像在点P(1,m)处的切线方程为
的图像在点P(1,m)处的切线方程为 ,则m的值为( )
,则m的值为( )
A.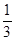 | B.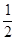 | C.-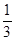 | D.-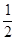 |
设函数 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为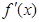 ,且有
,且有 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
若函数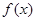 在R上可导,且
在R上可导,且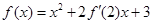 ,则( )
,则( )
A.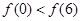 | B.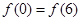 | C.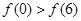 | D.无法确定 |
 的部分图象大致为( ).
的部分图象大致为( ).
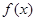 在定义域内可导,
在定义域内可导, 的图象如下右图所示,则导函数
的图象如下右图所示,则导函数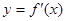 可能为( )
可能为( ) 