题目内容
函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有f(x1)≤f(x2),则称函数f(x)在D上为非减函数.设函数f(x)在[0,1]上为非减函数,且满足以下三个条件:
(1)f(0)=0
(2)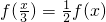
(3)f(1-x)=1-f(x).则 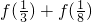 =________.
=________.
解:∵函数f(x)在[0,1]上为非减函数,①f(0)=0;③f(1-x)+f(x)=1,∴f(1)=1,
令x= ,所以有f(
,所以有f( )=
)= ,
,
又∵②f( )=
)= f(x),令x=1,有f(
f(x),令x=1,有f( )=
)= f(1)=
f(1)= ,
,
令x= ,有f(
,有f( )=
)= f(
f( )=
)= ,f(
,f( )=
)= f(
f( )=
)= ,
,
非减函数性质:当x1<x2时,都有f(x1)≤f(x2),∴ <
< <
< ,有f(
,有f( )≤f(
)≤f( )≤f(
)≤f( ),
),
而f( )=
)= =f(
=f( ),所以有 f(
),所以有 f( )=
)= ,则
,则 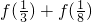 =
= .
.
故答案为:
分析:已知条件求出f(1)、f( )、f(
)、f( )、f(
)、f( )、f(
)、f( )的值,利用当x1<x2时,都有f(x1)≤f(x2),可求出f(
)的值,利用当x1<x2时,都有f(x1)≤f(x2),可求出f( )的值,从而求出所求.
)的值,从而求出所求.
点评:本题主要考查了抽象函数及其应用,以及新定义的理解,同时考查了计算能力和转化的思想,属于中档题.
令x=
 ,所以有f(
,所以有f( )=
)= ,
,又∵②f(
 )=
)= f(x),令x=1,有f(
f(x),令x=1,有f( )=
)= f(1)=
f(1)= ,
,令x=
 ,有f(
,有f( )=
)= f(
f( )=
)= ,f(
,f( )=
)= f(
f( )=
)= ,
,非减函数性质:当x1<x2时,都有f(x1)≤f(x2),∴
 <
< <
< ,有f(
,有f( )≤f(
)≤f( )≤f(
)≤f( ),
),而f(
 )=
)= =f(
=f( ),所以有 f(
),所以有 f( )=
)= ,则
,则 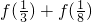 =
= .
.故答案为:

分析:已知条件求出f(1)、f(
 )、f(
)、f( )、f(
)、f( )、f(
)、f( )的值,利用当x1<x2时,都有f(x1)≤f(x2),可求出f(
)的值,利用当x1<x2时,都有f(x1)≤f(x2),可求出f( )的值,从而求出所求.
)的值,从而求出所求.点评:本题主要考查了抽象函数及其应用,以及新定义的理解,同时考查了计算能力和转化的思想,属于中档题.

练习册系列答案
相关题目
若函数f(x)的定义域为[-1,2],则函数
的定义域为( )
| f(x+2) |
| x |
| A、[-1,0)∪(0,2] |
| B、[-3,0) |
| C、[1,4] |
| D、(0,2] |