题目内容
【题目】已知定点
，横坐标不小于
的动点在
轴上的射影为
，若
.
（1）求动点
的轨迹
的方程；
（2）若点
不在直
线上，并且直线
与曲线相交于
两个不同点.问是否存在常数
使得当
的值变化时，直线
斜率之和是一个定值.若存在，求出的值；若不存在，请说明理由.
【答案】（1）
（2）见解析
【解析】
(1)利用抛物线定义，即可得到动点
的轨迹
的方程；
(2) 设
，则
，利用韦达定理即可得到结果.
（1）设点在直线
上的射影是
，则由于的横坐标不小于
，
所以
，又
所以
即点到
的距离与到直线的距离相等，所以的轨迹是以为焦点，以为准线的抛物线.
即的方程是
（2）由于
在曲线
上，可设，则
的斜率
的斜率
所以
又曲线与直线
相交于两点，所以
，于是联立方程，得
，所以
.
∴
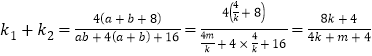=1-
，
此式随着m的变化，值也在变化，所以不存在k值满足题意.
练习册系列答案
相关题目
【题目】某小区为了调查居民的生活水平，随机从小区住户中抽取
个家庭，得到数据如下：
家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x（千元） | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y（千元） | 4 | 5 | 6 | 8 | 8 | 11 |
参考公式：回归直线的方程是：
，其中，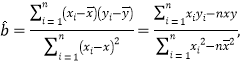
.
（1）据题中数据，求月支出
（千元）关于月收入
（千元）的线性回归方程（保留一位小数）；
（2）从这个家庭中随机抽取
个，求月支出都少于
万元的概率.
