题目内容
13.已知点B(4,0)、C(2,2),平面直角坐标系上的动点P满足$\overrightarrow{OP}=λ•\overrightarrow{OB}+μ•\overrightarrow{OC}$(其中O是坐标原点,且1<λ≤a,1<μ≤b),若动点P组成的区域的面积为8,则a+b的最小值是4.分析 先作向量$a•\overrightarrow{OB},b•\overrightarrow{OC}$,结合图形,根据λ,μ的范围找到动点P所在的区域:平行四边形FGHI,由向量$\overrightarrow{OB},\overrightarrow{OC}$求出sin∠BOC,求平行四边形FGHI,从而可得到$\frac{1}{a}+\frac{1}{b}=1$,从而a+b=(a+b)$(\frac{1}{a}+\frac{1}{b})$,根据基本不等式即可求得a+b的最小值.
解答 解:如图,在x轴上取点D,使|OD|=a|OB|,延长OC到E,使|OE|=b|OC|;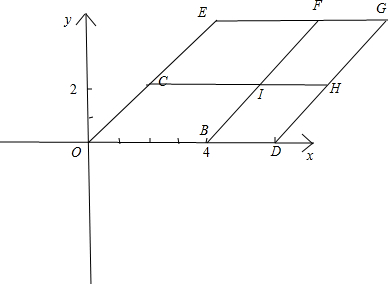 作CH∥OD,BF∥OE,EG∥OD,DG∥OE,则:
作CH∥OD,BF∥OE,EG∥OD,DG∥OE,则:
动点P组成的区域为平行四边形FGHI及其内部;
∵$\overrightarrow{OB}=(4,0),\overrightarrow{OC}=(2,2)$;
∴$cos∠BOC=\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|}=\frac{8}{8\sqrt{2}}=\frac{\sqrt{2}}{2}$;
∴$sin∠BOC=\frac{\sqrt{2}}{2}$;
∴${S}_{四边形FGHI}=(a-1)•4•(b-1)•2\sqrt{2}•\frac{\sqrt{2}}{2}=8$;
∴(a-1)•(b-1)=1;
∴ab-a-b=0;
∴$\frac{1}{a}+\frac{1}{b}=1$;
∴$a+b=(a+b)(\frac{1}{a}+\frac{1}{b})=2+\frac{a}{b}+\frac{b}{a}≥4$,当a=b=2时取“=”;
∴a+b的最小值为4.
故答案为:4.
点评 考查数乘的几何意义,平面向量基本定理,根据点的坐标求向量的坐标,向量夹角余弦公式的坐标运算,数量积的坐标运算,平行四边形的面积公式,以及基本不等式用于求最值.

| 优秀 | 良好 | 合格 | |
| 男 | 180 | 70 | 20 |
| 女 | 120 | a | 30 |
(1)求a的值;
(2)若用分层抽样的方法,在合格的员工中按男女抽取一个容量为5的样本,从中任选2人,求抽取两人刚好是一男一女的概率.
| 测试指杯 | [80,84) | [84,88) | [88,92) | [92.96) | [96,100】 |
| 产品A | 6 | 14 | 42 | 31 | 7 |
| 产品B | 8 | 17 | 40 | 30 | 5 |
(Ⅱ)生产1件产品A,若是合格品则盈利45元.若是次品则亏损10元;生产1件产品B,若是合格品则盈利60元.若是次品则亏损15元;在(Ⅰ)的前提下,(i)X为生产1件产品A和1件产品B所得的总利润,求随机变量的分布列和数学期望;(ii)求生产5件产品B所得利润不少于150元的概率.
 如图,PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交OP于点D,证明:
如图,PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交OP于点D,证明: