题目内容
已知函数 (
( 为常数).
为常数).
(1)当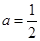 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)若 ,且对任意的
,且对任意的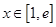 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)函数 的单调递减区间为
的单调递减区间为 ;(2)实数
;(2)实数 的取值范围是
的取值范围是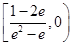 .
.
解析试题分析:(1)将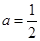 代入函数解析式并求出相应的导数,利用导数并结合函数的定义域便可求出函数的单调递减区间;(2)构造新函数
代入函数解析式并求出相应的导数,利用导数并结合函数的定义域便可求出函数的单调递减区间;(2)构造新函数 ,将问题转化为“对任意
,将问题转化为“对任意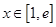 时,
时,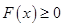 恒成立”,进而转化为
恒成立”,进而转化为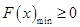 ,围绕
,围绕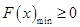 这个核心问题结合分类讨论的思想求出参数
这个核心问题结合分类讨论的思想求出参数 的取值范围.
的取值范围.
试题解析:(1) 的定义域为
的定义域为 ,
, ,
,
当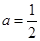 时,
时, , 2分
, 2分
由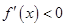 及
及 ,解得
,解得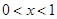 ,所以函数
,所以函数 的单调递减区间为
的单调递减区间为 4分
4分
(2)设 ,
,
因为对任意的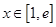 ,
, 恒成立,所以
恒成立,所以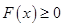 恒成立,
恒成立, ,
,
因为 ,令
,令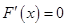 ,得
,得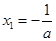 ,
, , 7分
, 7分
①当 ,即
,即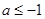 时,
时,
因为 时,
时,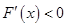 ,所以
,所以 在
在 上单调递减,
上单调递减,
因为对任意的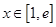 ,
,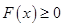 恒成立,
恒成立,
所以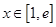 时,
时, ,即
,即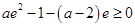 ,
,
解得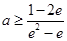 ,因为
,因为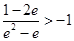 。所以此时
。所以此时 不存在; 10分
不存在; 10分
②当 ,即
,即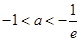 时,因为
时,因为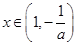 时,
时,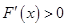 ,
, 时,
时,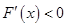 ,
,
所以 在
在 上单调递增,在
上单调递增,在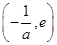 上单调递减,
上单调递减,
因为对任意的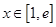 ,
,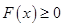 恒成立,所以
恒成立,所以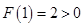 ,且
,且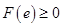 ,
,
即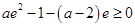 ,解得
,解得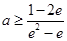 ,
,
因为 ,所以此时
,所以此时 ; 13分
; 13分
③当 ,即
,即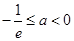 时,因为
时,因为 时,
时,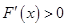 ,
,
所以 在
在 上单调递增,由于
上单调递增,由于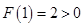 ,符合题意; 15分
,符合题意; 15分
综上所述,实数 的取值范围是
的取值范围是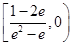 16分
16分
考点:函数的单调区间与导数、不等式恒成立、分类讨论

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.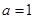 时,求函数
时,求函数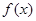 的极值;
的极值;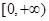 上单调递增,试求
上单调递增,试求 的取值或取值范围
的取值或取值范围 ,
,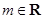 .
.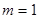 时,求曲线
时,求曲线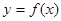 在点
在点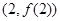 处的切线方程;
处的切线方程;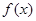 在区间
在区间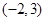 上是减函数,求
上是减函数,求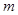 的取值范围.
的取值范围. (
( 是自然对数的底数).
是自然对数的底数). 在
在 处的切线也是抛物线
处的切线也是抛物线 的切线,求
的切线,求 的值;
的值; 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点 处的切线斜率与
处的切线斜率与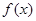 在
在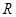 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.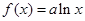 ,
, .
.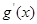 为
为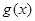 的导函数,若不等式
的导函数,若不等式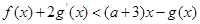 在
在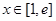 上有解,求实数
上有解,求实数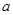 的取值范围;
的取值范围;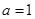 ,对任意的
,对任意的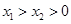 ,不等式
,不等式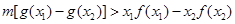 恒成立.求
恒成立.求 (
( ,
, )的值.
)的值.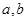 是实数,函数
是实数,函数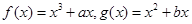 ,
,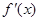 和
和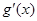 ,分别是
,分别是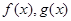 的导函数,若
的导函数,若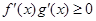 在区间
在区间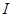 上恒成立,则称
上恒成立,则称 和
和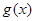 在区间
在区间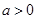 ,若函数
,若函数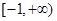 上单调性一致,求实数
上单调性一致,求实数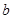 的取值范围;
的取值范围;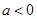 且
且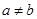 ,若函数
,若函数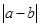 的最大值.
的最大值. .
.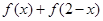 的值是否为定值?若是,求出该定值;若不是,请说明理由;
的值是否为定值?若是,求出该定值;若不是,请说明理由;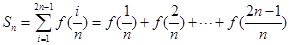 ,其中
,其中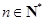 ,求
,求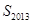 ;
;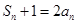 .若不等式
.若不等式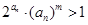 对
对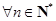 且
且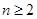 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
.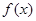 的单调区间;
的单调区间;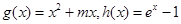 ,若在
,若在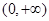 上至少存在一点
上至少存在一点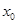 ,使得
,使得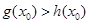 成立,求
成立,求 的范围.
的范围.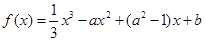 (
(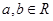 ),其图像在点(1,
),其图像在点(1,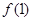 )处的切线方程为
)处的切线方程为 .
.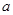 ,
,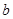 的值;
的值;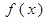 的单调区间和极值;
的单调区间和极值;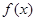 在区间[-2,5]上的最大值.
在区间[-2,5]上的最大值.