题目内容
直线m，n，l交于一点，经过这3条直线的平面（ ）
分析：设由相交直线m、n交于点O，它们确定的平面记为α，则直线l必定经过点O．然后讨论：当直线l在平面α内经过点O时，可得经过直线m、n、l的平面有且只有一个；当直线l经过平面α内点O，并且与平面α相交时，不存在经过直线m、n、l的平面．由此可得正确选项．
解答：解：∵直线m，n是相交直线，
∴设m、n相交于点O，由m、n确定的平面记为α，
又∵直线m，n，l交于一点，
∴直线l经过点O
①当直线l在平面α内经过点O时，
经过直线m、n、l的平面有且只有平面α一个；
②当直线l经过平面α内点O，并且与平面α相交时，
由相交直线m、l确定一个平面β，由相交直线n、l确定一个平面γ，
并且α、β、γ是互不重合的平面，
这样经过直线m、n、l的平面0个．
综上所述，经过直线m、n、l的平面有一个或0个．
故选C
∴设m、n相交于点O，由m、n确定的平面记为α，
又∵直线m，n，l交于一点，
∴直线l经过点O
①当直线l在平面α内经过点O时，
经过直线m、n、l的平面有且只有平面α一个；
②当直线l经过平面α内点O，并且与平面α相交时，
由相交直线m、l确定一个平面β，由相交直线n、l确定一个平面γ，
并且α、β、γ是互不重合的平面，
这样经过直线m、n、l的平面0个．
综上所述，经过直线m、n、l的平面有一个或0个．
故选C
点评：本题通过三条直线相交于一点，能确定平面的个数为例，着重考查了平面的基本性质和空间两条直线的位置关系等知识点，属于基础题．
练习册系列答案
相关题目
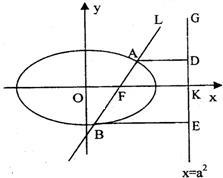如图，已知直线L：