题目内容
(2013•肇庆一模)已知圆C的方程为x2+y2+2x-7=0,圆心C关于原点对称的点为A,P是圆上任一点,线段AP的垂直平分线l交PC于点Q.
(1)当点P在圆上运动时,求点Q的轨迹L的方程;
(2)过点B(1,
)能否作出直线l2,使l2与轨迹L交于M、N两点,且点B是线段MN的中点,若这样的直线l2存在,请求出它的方程和M、N两点的坐标;若不存在,请说明理由.
(1)当点P在圆上运动时,求点Q的轨迹L的方程;
(2)过点B(1,
| 1 | 2 |
分析:(1)由点Q是线段AP的垂直平分线l与CP的交点,可得|QP|=QA|.又|PQ|+|QC|=2
,可得|QA|+|QC|=2
>AC=2.利用椭圆的定义可知点Q的轨迹L为椭圆;
(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入
+y2=1,利用“点差法”、中点坐标公式及斜率公式即可得出直线l2的方程;与椭圆方程联立即可解得交点坐标.
| 2 |
| 2 |
(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入
| x2 |
| 2 |
解答:解:(1)如图,由已知圆C的方程x2+y2+2x-7=0,化为(x+1)2+y2=8,可得圆心C(-1,0),半径r=2
,点A(1,0).
∵点Q是线段AP的垂直平分线l与CP的交点,∴|QP|=QA|.
又∵|PQ|+|QC|=2
,∴|QA|+|QC|=2
>AC=2.
∴点Q的轨迹是以O为中心,C,A为焦点的椭圆,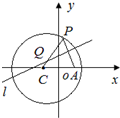
∵c=1,a=
,∴b=
=1,
∴点Q的轨迹L的方程为
+y2=1.
(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入
+y2=1得
,
两式相减得
=-(y1-y2)(y1+y2),即
=-
×
.
由题意,得x1+x2=2,y1+y2=1,
∴
=-1,即kMN=-1.
∴直线l2的方程为y=-x+
.
由
得6x2-12x+5=0.
∵点B在椭圆L内,
∴直线l2的方程为y=-x+
,它与轨迹L存在两个交点,
解方程6x2-12x+5=0得x=1±
.
当x=1+
时,y=
-
;当x=1-
时,y=
+
.
所以,两交点坐标分别为(1+
,
-
)和(1-
,
+
).
| 2 |
∵点Q是线段AP的垂直平分线l与CP的交点,∴|QP|=QA|.
又∵|PQ|+|QC|=2
| 2 |
| 2 |
∴点Q的轨迹是以O为中心,C,A为焦点的椭圆,

∵c=1,a=
| 2 |
| a2-c2 |
∴点Q的轨迹L的方程为
| x2 |
| 2 |
(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入
| x2 |
| 2 |
|
两式相减得
| (x1-x2)(x1+x2) |
| 2 |
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
| x1+x2 |
| y1+y2 |
由题意,得x1+x2=2,y1+y2=1,
∴
| y1-y2 |
| x1-x2 |
∴直线l2的方程为y=-x+
| 3 |
| 2 |
由
|
∵点B在椭圆L内,
∴直线l2的方程为y=-x+
| 3 |
| 2 |
解方程6x2-12x+5=0得x=1±
| ||
| 6 |
当x=1+
| ||
| 6 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 6 |
| 1 |
| 2 |
| ||
| 6 |
所以,两交点坐标分别为(1+
| ||
| 6 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 6 |
| 1 |
| 2 |
| ||
| 6 |
点评:本题综合考查了椭圆的定义、标准方程及其性质、“点差法”、中点坐标公式、直线与椭圆相交问题转化为方程联立得到一元二次方程等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力.

练习册系列答案
相关题目
 (2013•肇庆一模)某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了x•46%=230人,回答问题统计结果如图表所示.
(2013•肇庆一模)某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了x•46%=230人,回答问题统计结果如图表所示.