题目内容
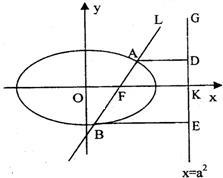 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)若抛物线x2=4
| 3 |
否则说明理由.
(文科生做)若N(
| a2+1 |
| 2 |
| AN |
| NE |
分析:(1)先由已知得b=
以及c=1,即可求出椭圆C的方程;
(2)(理科生做)先让m取0,求出点N的坐标,再猜想:当m变化时,AE与BD相交于此定点N.先利用斜率相等证明A、N、E三点共线同理可得B、N、D三点共线,即可证明结论.
(文科生做)直接求直线AN和直线NE的斜率,利用上面的过程得到二者斜率相等即可证明结论.
| 3 |
(2)(理科生做)先让m取0,求出点N的坐标,再猜想:当m变化时,AE与BD相交于此定点N.先利用斜率相等证明A、N、E三点共线同理可得B、N、D三点共线,即可证明结论.
(文科生做)直接求直线AN和直线NE的斜率,利用上面的过程得到二者斜率相等即可证明结论.
解答:解:(1)易知b=
⇒b2=3,
又F(1,0),c=1,∴a2=b2+c2=4.
所以椭圆C的方程为:
+
=1.
(2)(理科生做)因为F(1,0),k=(a2,0)
先探索,当m=0时,直线L⊥ox轴,则ABED为矩形,由对称性知,AE与BD相交于FK中点N,且N(
,0)
猜想:当m变化时,AE与BD相交于定点N(
,0).
证明:设设A(x1,y1),B(x2,y2),E(a2,y2),D(a2,y1),
当m变化时首先AE过定点N.
由
⇒(a2+b2m2)y2+2mb2y+b2(1-a2)=0.△4a2b2(a2+m2b2-1)>0,(因为a>1)
且.y1+y2=-
①,y1•y2=
②.
因为KAN=
,KEN=
,
所以kAN-KEN=
③,
把①②代入③整理得KAN-KEN=0.
∴KAN=KEN∴A、N、E三点共线同理可得B、N、D三点共线
∴AE与BD相交于定点N(
,0).
(文科生做).直接求出直线AN和直线NE的斜率,利用上面的推导过程可以得到二者斜率相等,故A、N、E三点共线.即可得:
=λ
.
| 3 |
又F(1,0),c=1,∴a2=b2+c2=4.
所以椭圆C的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)(理科生做)因为F(1,0),k=(a2,0)
先探索,当m=0时,直线L⊥ox轴,则ABED为矩形,由对称性知,AE与BD相交于FK中点N,且N(
| a2+1 |
| 2 |
猜想:当m变化时,AE与BD相交于定点N(
| a2+1 |
| 2 |
证明:设设A(x1,y1),B(x2,y2),E(a2,y2),D(a2,y1),
当m变化时首先AE过定点N.
由
|
且.y1+y2=-
| 2mb2 |
| a2+b2m2 |
| b2(1-a2) |
| a2+b2m2 |
因为KAN=
| -y1 | ||
|
| -y2 | ||
|
所以kAN-KEN=
| ||||
|
把①②代入③整理得KAN-KEN=0.
∴KAN=KEN∴A、N、E三点共线同理可得B、N、D三点共线
∴AE与BD相交于定点N(
| a2+1 |
| 2 |
(文科生做).直接求出直线AN和直线NE的斜率,利用上面的推导过程可以得到二者斜率相等,故A、N、E三点共线.即可得:
| AN |
| NE |
点评:题主要考查椭圆的标准方程,直线与椭圆的位置关系以及直线和直线之间的关系等基础知识,考查推理论证能力,运算求解能力及创新意识,考查化归与转化思想,数形结合思想以及特殊与一般思想.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 如图,已知直线l:x=my+1过椭圆
如图,已知直线l:x=my+1过椭圆 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2. 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: (2012•乐山二模)如图,已知直线L:x=my+1过椭圆C:
(2012•乐山二模)如图,已知直线L:x=my+1过椭圆C: