题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:∵ ∴ 即 又 所以 ∵ ∴ |
(2) |
解:由第一问可知 ∴
当n=7时, 当n<7时, 当n>7时, ∴当n=7或n=8时, |
(3) |
解:由 依题意(*)式对任意 ①当t=0时,(*)式显然不成立,因此t=0不合题意.…………9分 ②当t<0时,由 而当m是偶数时 ③当t>0时,由 ∴ 设 ∵ ∴ ∴ 所以实数 |

练习册系列答案
相关题目
| |||||||||||
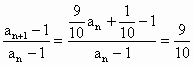 ,
,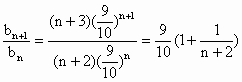 .……………………………5分
.……………………………5分