Question

已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），直线l为圆O：x²+y²=b²的一条切线，记椭圆C的离心率为e．
（1）若直线l的倾斜角为

π

3

，且恰好经过椭圆的右顶点，求e的大小；
（2）在（1）的条件下，设椭圆的上顶点为A，左焦点为F，过点A与AF垂直的直线交x轴的正半轴于B点，过A、B、F三点的圆恰好与直线l：x+

3

y+3=0相切，求椭圆方程．

Answer 1

分析：（1）设出直线l与圆O的切点为C，椭圆的右顶点为D，根据切线性质得到三角形OCD为直角三角形，且得到OC和OD及角ODC的度数，利用勾股定理及椭圆的简单性质a²=b²+c²表示出CD，根据余弦函数的定义以及离心率公式即可求出e的值；
（2）根据（1）求出的离心率及a²=b²+c²设出a和b，由字母m写出椭圆的标准方程，从而表示出点A的坐标，得到AF的长，求出直线AF的斜率，进而得到∠AFB等于60°，根据直角三角形中30°所对的直角边等于斜边的一半由AF的长表示出FB的长，从而得到点B的坐标，根据中点坐标公式求出FB中点G的坐标，然后根据直角三角形外接圆的圆心为斜边的中点，得到外接圆的半径，由直线与圆相切时圆心到直线的距离等于半径，利用点到直线的距离公式表示出点G到直线l的距离d，让d等于表示出的半径，列出关于m的方程，求出方程的解即可得到m的值，从而确定出椭圆的方程．

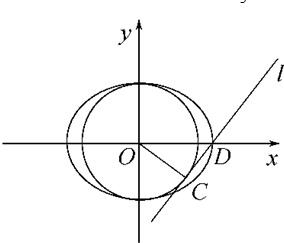
解答：解：（1）如图，设直线l与圆O相切于C点，椭圆的右顶点为D，则由题意知△OCD为直角三角形，
且OC=b，OD=a，∠ODC=

π

3

，
∴CD=

OD2-OC2

=

a2-b2

=c（c为椭圆的半焦距），
∴椭圆的离心率e=

c

a

=cos

π

3

=

1

2

．
（2）由（1）知，

c

a

=

1

2

，
∴设a=2m（m＞0），则b=

3

m，
∴椭圆方程为

x2

4m2

+

y2

3m2

=1．
∴A（0，

3

m），
∴AF=2m，k_AF=

3

，
∴∠AFB=60°，
在Rt△AFB中，有FB=4m，
∴B（3m，0），设FB的中点为G，则G（m，0），
∵△AFB为直角三角形，
∴过A、B、F三点的圆的圆心为斜边FB的中点G，且半径为2m，
∵圆G与直线l：x+

3

y+3=0相切，
∴

|m+3|

1+3

=2m，
∵m是大于0的常数，
∴m=1，故所求的椭圆方程为

x2

4

+

y2

3

=1．

点评：本题主要考查椭圆的几何性质，直线与圆的位置关系及直角三角形的性质等基础知识，同时考查解析几何的基本思想方法和运算求解能力．根据第一问的结论设出椭圆的方程是解本题的关键，求解方法是待定系数法．