��Ŀ����
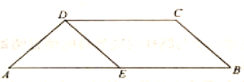
����Ŀ����![]() ƽ���ϣ���������Բ��
ƽ���ϣ���������Բ��![]() ��
��![]() ������ֱ��
������ֱ��![]() ��
��![]() Χ�ɵķ��ͼ�μ�Ϊ
Χ�ɵķ��ͼ�μ�Ϊ![]() ����ͼ����Ӱ����.��
����ͼ����Ӱ����.��![]() ��
��![]() ����תһ�ܶ��ɵļ�����Ϊ
����תһ�ܶ��ɵļ�����Ϊ![]() ����
����![]() ��
��![]() ��ˮƽ���棬���ý������Ϊ
��ˮƽ���棬���ý������Ϊ![]() ���������敜ԭ�����敜ԭ���������Ƽ�ͬ����������족����˼�ǣ����ȸߵļ�������ͬ�ߴ����صõ����������������ȣ���ô������������������ȣ���һ��ƽ�ŵ�Բ����һ�������壬�ó�
���������敜ԭ�����敜ԭ���������Ƽ�ͬ����������족����˼�ǣ����ȸߵļ�������ͬ�ߴ����صõ����������������ȣ���ô������������������ȣ���һ��ƽ�ŵ�Բ����һ�������壬�ó�![]() �����ֵΪ__________��
�����ֵΪ__________��

���𰸡�![]()
��������
����Ŀ������![]() ��ˮƽ�����������ɲ���ˮƽ���õ�Բ���ͳ����������Ȼ��ֱ�����Բ��������볤�����������ͼ���.
��ˮƽ�����������ɲ���ˮƽ���õ�Բ���ͳ����������Ȼ��ֱ�����Բ��������볤�����������ͼ���.
��Ϊ������![]() ��ˮƽ����Ľ������Ϊ
��ˮƽ����Ľ������Ϊ![]() ���ý���Ľ����������������ɣ�һ����Ϊ��ֵ
���ý���Ľ����������������ɣ�һ����Ϊ��ֵ![]() �������ǽ�һ�������Ϊ
�������ǽ�һ�������Ϊ![]() ����Ϊ2�ij�����õ��ģ�����
����Ϊ2�ij�����õ��ģ�����![]() �������ǰ�һ���뾶Ϊ1����Ϊ
�������ǰ�һ���뾶Ϊ1����Ϊ![]() ��Բ���õ��ģ���ͼ��ʾ��
��Բ���õ��ģ���ͼ��ʾ��
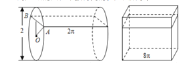
�������������![]() ����һ�𣬸����敜ԭ����ÿ��ƽ��ˮƽ��Ľ��������ȣ������������ȣ���
����һ�𣬸����敜ԭ����ÿ��ƽ��ˮƽ��Ľ��������ȣ������������ȣ���![]() �����Ϊ
�����Ϊ![]() .����
.����![]() .
.

��ϰ��ϵ�д�
 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
�����Ŀ