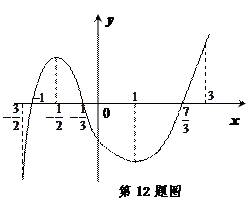
题目内容
(本题9分)设函数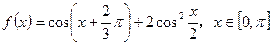 。
。
(1)求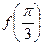 的值;
的值;
(2)求 的最小值及
的最小值及 取最小值时
取最小值时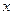 的集合;(3)求
的集合;(3)求 的单调递增区间。
的单调递增区间。
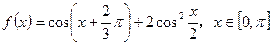 。
。(1)求
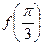 的值;
的值;(2)求
 的最小值及
的最小值及 取最小值时
取最小值时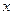 的集合;(3)求
的集合;(3)求 的单调递增区间。
的单调递增区间。解:(1)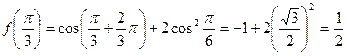 。………3分
。………3分
(2)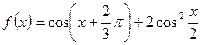
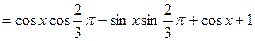
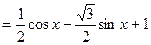
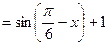 。
。
因为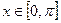 ,所以
,所以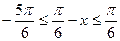 ,所以
,所以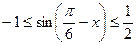 。
。
所以函数 的最小值为0。
的最小值为0。
此时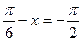 ,即
,即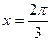 。所以
。所以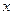 的取值集合为
的取值集合为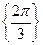 。
。 ……………6分
……………6分
(3)由(2)可知: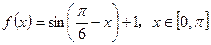 。
。
设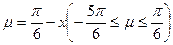 ,则原函数为
,则原函数为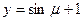 。
。
因为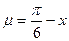 为减函数,所以
为减函数,所以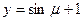 的减区间就是复合函数
的减区间就是复合函数 的增区间。
的增区间。
由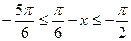 ,得
,得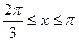 。
。
所以,函数 的单调递增区间是
的单调递增区间是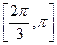 。………………………………………9分
。………………………………………9分
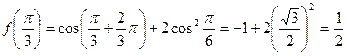 。………3分
。………3分(2)
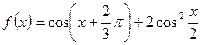
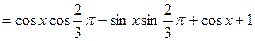
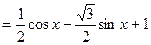
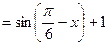 。
。因为
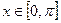 ,所以
,所以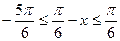 ,所以
,所以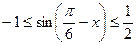 。
。所以函数
 的最小值为0。
的最小值为0。此时
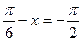 ,即
,即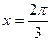 。所以
。所以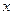 的取值集合为
的取值集合为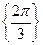 。
。 ……………6分
……………6分(3)由(2)可知:
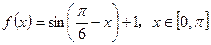 。
。设
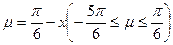 ,则原函数为
,则原函数为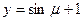 。
。因为
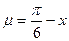 为减函数,所以
为减函数,所以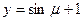 的减区间就是复合函数
的减区间就是复合函数 的增区间。
的增区间。由
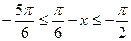 ,得
,得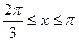 。
。所以,函数
 的单调递增区间是
的单调递增区间是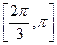 。………………………………………9分
。………………………………………9分略

练习册系列答案
相关题目
 ,2)时,(x-2)
,2)时,(x-2)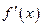 >0.设a=f(1
>0.设a=f(1 ),
),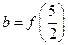 ,c=f(4),则a,b,c的大小为 .
,c=f(4),则a,b,c的大小为 .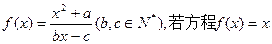 有且只有两个相异实根0,2,且
有且只有两个相异实根0,2,且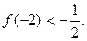
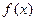 的解析式;
的解析式; 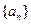 满足
满足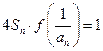 ,求通
,求通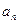 ,
,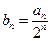 ,求数列
,求数列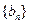 的前
的前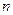 项和
项和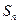 .
.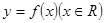 是可导的函数,若满足
是可导的函数,若满足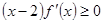 ,则必有
,则必有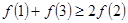
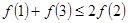
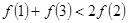
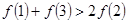
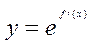 的图象如下图所示,
的图象如下图所示,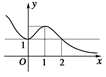
 方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
方体的长、宽、高各为多少时,其体积最大?最大体积是多少?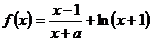 ,其中实数
,其中实数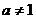 。
。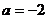 ,求曲线
,求曲线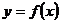 在点
在点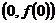 处的切线方程;
处的切线方程;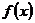 在
在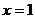 处取得极值,试讨论
处取得极值,试讨论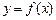 的定义域为
的定义域为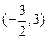 ,且
,且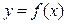 的图像如右图所示,记
的图像如右图所示,记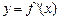 ,则不等式
,则不等式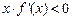 的解集是 ▲ .
的解集是 ▲ .