题目内容
12.为响应国家号召开展“社会实践活动”,某校高二(8)班学生对本县住宅楼房屋销售价格y和房屋面积x的统计有关数据如下:| 房屋面积(m) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(Ⅰ)画出数据对应的散点图;
(Ⅱ)设线性回归方程为$\widehat{y}$=bx+a,已计算得b=0.196,$\overline{y}$=23.2,计算$\overline{x}$及a;
(Ⅲ)某同学家人计划在本县购置一套面积为诶120m2的房子,且一次付清,根据(Ⅱ)的结果,估计房屋的销售价格.
分析 (I)根据表中所给的五对数据,在平面直角坐标系中描出这五个点,得到这组数据的散点图.
(II)根据表中所给的数据,求出横标的平均数,把求得的数据代入求线性回归方程的系数的公式,利用最小二乘法得到结果,写出线性回归方程.
(III)根据第二问求得的线性回归方程,代入所给的x的值,预报出销售价格的估计值,这个数字不是一个准确数值.
解答 解:(I)根据表中所给的数据,写出对应的点的坐标,画出对应的散点图如下图所示:
 …(3分)
…(3分)
(Ⅱ)∵$\overline{x}$=$\frac{1}{5}$$\sum_{i=1}^{5}{x}_{i}$=109,
∴a=$\overline{y}$-b$\overline{x}$=23.2-109×0.196=1.836.….(7分)
(Ⅲ)由(Ⅱ)知,回归直线方程为$\widehat{y}$=0.196x+1.836.…..(9分)
所以,当x=120m2时,销售价格的估计值为:$\widehat{y}$=0.196×120+1.836=25.356(万元)
所以面积为120m2的房屋销售价格估计为25.356万元.…(12分)
点评 本题考查线性回归分析,考查散点图和估计y的值,本题解题的关键是正确求出横标的平均数,得到样本中心点,在一些题目中正确运算时解题的关键,本题是一个中档题目.

练习册系列答案
相关题目
20.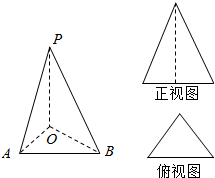 若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
 若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
7.若直线y=x+k与曲线x=$\sqrt{1-{y}^{2}}$恰有一个公共点,则k的取值范围是( )
| A. | k=-$\sqrt{2}$或-1<k≤1 | B. | k≥$\sqrt{2}$或k≤-$\sqrt{2}$ | C. | -$\sqrt{2}$<k<$\sqrt{2}$ | D. | k=±$\sqrt{2}$ |
17.已知{an}是等比数列,a1=8,a4=1,则公比q=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
4.在等差数列{an}中,a1,a2015为方程x2-20x+16=0的两根,则a2+a1008+a2014=( )
| A. | 40 | B. | 36 | C. | 30 | D. | 24 |
2.下列函数中,在区间(0,+∞)上增长速度越来越快的是( )
| A. | y=20071nx | B. | y=x2007 | C. | y=$\frac{{e}^{x}}{2007}$ | D. | y=2007•2x |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位,所得曲线的一部分如图所示,f(x)的周期为π,φ的值为-$\frac{π}{3}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位,所得曲线的一部分如图所示,f(x)的周期为π,φ的值为-$\frac{π}{3}$.