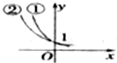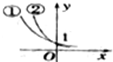题目内容
7.若直线y=x+k与曲线x=$\sqrt{1-{y}^{2}}$恰有一个公共点,则k的取值范围是( )| A. | k=-$\sqrt{2}$或-1<k≤1 | B. | k≥$\sqrt{2}$或k≤-$\sqrt{2}$ | C. | -$\sqrt{2}$<k<$\sqrt{2}$ | D. | k=±$\sqrt{2}$ |
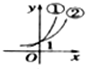
分析 曲线x=$\sqrt{1-{y}^{2}}$表示一个半圆(单位圆位于x轴及x轴右侧的部分).当直线y=x+k经过点A、B时,分别求得k的值,再求出当直线y=x+k和半圆相切时k的值,数形结合求得k的范围.
解答  解:曲线x=$\sqrt{1-{y}^{2}}$,即x2+y2=1 (x≥0),表示一个半圆(单位圆位于x轴及x轴右侧的部分).
解:曲线x=$\sqrt{1-{y}^{2}}$,即x2+y2=1 (x≥0),表示一个半圆(单位圆位于x轴及x轴右侧的部分).
如图,A(0,1)、B(1,0)、C(0,-1),
当直线y=x+k经过点A时,1=0+k,求得 k=1;
当直线y=x+k经过点B、点C时,0=1+k,求得 k=-1;
当直线y=x+k和半圆相切时,由圆心到直线的距离等于半径,
可得1=$\frac{|0-0+k|}{\sqrt{2}}$,求得k=-$\sqrt{2}$,或k=$\sqrt{2}$(舍去),
故要求的实数k的范围为k=-$\sqrt{2}$或-1<k≤1
故选:A.
点评 本题主要考查直线和圆的位置关系,直线和圆相切的性质,点到直线的距离公式的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
12.为响应国家号召开展“社会实践活动”,某校高二(8)班学生对本县住宅楼房屋销售价格y和房屋面积x的统计有关数据如下:
(可能用到的公式:)b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$
(Ⅰ)画出数据对应的散点图;
(Ⅱ)设线性回归方程为$\widehat{y}$=bx+a,已计算得b=0.196,$\overline{y}$=23.2,计算$\overline{x}$及a;
(Ⅲ)某同学家人计划在本县购置一套面积为诶120m2的房子,且一次付清,根据(Ⅱ)的结果,估计房屋的销售价格.
| 房屋面积(m) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(Ⅰ)画出数据对应的散点图;
(Ⅱ)设线性回归方程为$\widehat{y}$=bx+a,已计算得b=0.196,$\overline{y}$=23.2,计算$\overline{x}$及a;
(Ⅲ)某同学家人计划在本县购置一套面积为诶120m2的房子,且一次付清,根据(Ⅱ)的结果,估计房屋的销售价格.
19.某单位有职工750人,其中青年职工420人,中年职工210人,老年职工120人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为14人,则样本容量为( )
| A. | 7 | B. | 15 | C. | 25 | D. | 35 |
16.下列函数中,定义域与值域相同的是( )
| A. | y=$\frac{2}{x}$ | B. | y=x2 | C. | y=log2x | D. | y=2x |