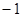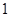题目内容
已知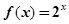
 可以表示为一个奇函数
可以表示为一个奇函数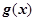 与一个偶函数
与一个偶函数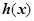 之和,若不等式
之和,若不等式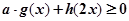 对于
对于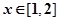 恒成立,则实数
恒成立,则实数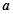 的取值范围是____________.
的取值范围是____________.
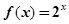
 可以表示为一个奇函数
可以表示为一个奇函数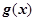 与一个偶函数
与一个偶函数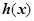 之和,若不等式
之和,若不等式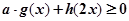 对于
对于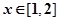 恒成立,则实数
恒成立,则实数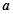 的取值范围是____________.
的取值范围是____________.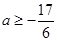
试题分析:依题意,g(x)+h(x)=
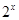 .....(1),∵g(x)是奇函数,∴g(-x)=-g(x);∵h(x)是偶函数,∴h(-x)=h(x);
.....(1),∵g(x)是奇函数,∴g(-x)=-g(x);∵h(x)是偶函数,∴h(-x)=h(x);∴g(-x)+h(-x)="h(x)-g(x)="
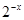 ......(2)
......(2)解(1)和(2)组成的方程组得h(x)=
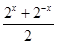 ,g(x)=
,g(x)= 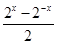
∴ag(x)+h(2x)=a
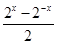 +
+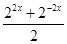 ,∴a·
,∴a·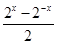 +
+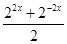 ≥0在x∈[1,2]恒成立
≥0在x∈[1,2]恒成立令t=
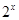 ,∴
,∴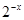 =
= ,当x∈[1,2]时,t∈[2,4],
,当x∈[1,2]时,t∈[2,4],∴原不等式化为a(t-
 )+(t2+
)+(t2+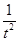 )≥0在t∈[2,4]上恒成立,由不等式a(t-
)≥0在t∈[2,4]上恒成立,由不等式a(t- )+(t2+
)+(t2+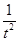 )≥0,
)≥0,可得a(t-
 )≥-(t2+
)≥-(t2+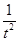 ),∵当t∈[2,4]时,t-
),∵当t∈[2,4]时,t- t>0恒成立,∴a≥
t>0恒成立,∴a≥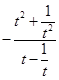 =
=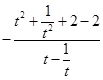 =
= 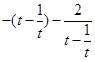 ,即a≥
,即a≥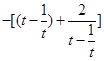 在t∈[2,4]上恒成立,
在t∈[2,4]上恒成立,令u=t-
 ,求导得
,求导得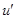 =1+
=1+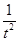 >0恒成立,∴u=t-
>0恒成立,∴u=t- 在t∈[2,4]上单调递增
在t∈[2,4]上单调递增∴u∈[
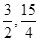 ],令f(u)=u+
],令f(u)=u+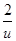 ,u∈[
,u∈[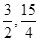 ],
],求导得
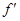 (u)=1-
(u)=1-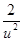 >0在u∈[
>0在u∈[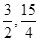 ]上恒成立,∴f(u)在u∈[
]上恒成立,∴f(u)在u∈[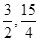 ]上单调递增
]上单调递增即当u=
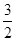 ,f(u)取最小值f(
,f(u)取最小值f(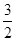 )=
)= 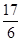 ,
,当u=
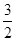 时,可解得t=2(另一根不在t∈[2,4]内故舍去)
时,可解得t=2(另一根不在t∈[2,4]内故舍去)∴当t=2时,
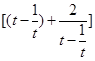 取最小值为
取最小值为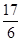 ,即
,即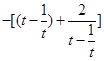 取最大值为-
取最大值为-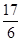 ,∴a≥-
,∴a≥-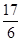 ,当t=2,x=1时取等号,∴a的最小值为-
,当t=2,x=1时取等号,∴a的最小值为-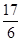 .
.
练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
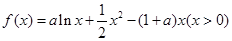 .
.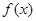 的单调区间;
的单调区间;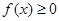 在
在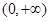 内恒成立,求实数
内恒成立,求实数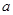 的取值范围.
的取值范围.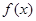 是
是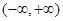 上的偶函数,若对于
上的偶函数,若对于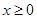 ,都有
,都有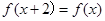 ,且当
,且当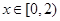 时,
时,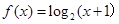 ,则
,则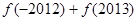 =____________.
=____________.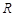 上的函数
上的函数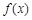 ,对任意
,对任意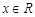 都有
都有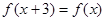 ,当
,当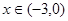 时,
时,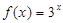 ,则
,则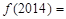 .
.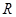 上的函数
上的函数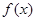 是偶函数,对
是偶函数,对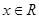 都有
都有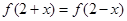 ,当
,当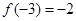 时,
时,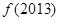 的值为( )
的值为( )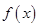 是定义在
是定义在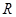 上的偶函数,当
上的偶函数,当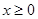 时,
时,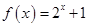 .若
.若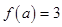 ,则实数
,则实数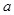 的值为 .
的值为 .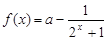 ,且
,且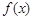 为奇函数,则
为奇函数,则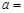 .
.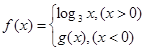 ,若
,若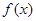 是奇函数,则
是奇函数,则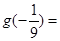 .
.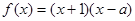 为偶函数,则
为偶函数,则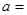 ( )
( )