题目内容
已知函数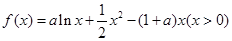 .
.
(Ⅰ)求函数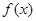 的单调区间;
的单调区间;
(Ⅱ)若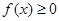 在
在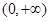 内恒成立,求实数
内恒成立,求实数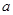 的取值范围.
的取值范围.
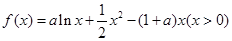 .
.(Ⅰ)求函数
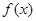 的单调区间;
的单调区间;(Ⅱ)若
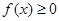 在
在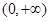 内恒成立,求实数
内恒成立,求实数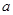 的取值范围.
的取值范围.(Ⅰ)当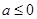 时,
时,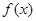 在
在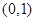 单调递减,在
单调递减,在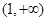 上单调递增;
上单调递增;
当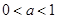 时,
时,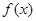 在
在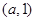 单调递减,在
单调递减,在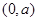 ,
,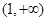 上单调递增;
上单调递增;
当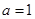 时,
时,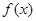 在
在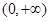 上单调递增;
上单调递增;
当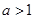 时,
时,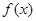 在
在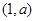 单调递减, 在
单调递减, 在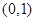 ,
,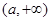 上单调递增;
上单调递增;
(Ⅱ)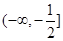
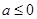 时,
时,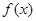 在
在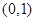 单调递减,在
单调递减,在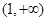 上单调递增;
上单调递增;当
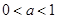 时,
时,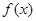 在
在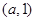 单调递减,在
单调递减,在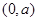 ,
,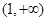 上单调递增;
上单调递增;当
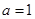 时,
时,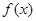 在
在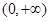 上单调递增;
上单调递增;当
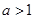 时,
时,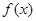 在
在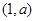 单调递减, 在
单调递减, 在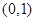 ,
,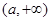 上单调递增;
上单调递增;(Ⅱ)
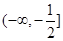
试题分析:(Ⅰ)利用导数的符号确定函数的单调区间。函数含有参数,故需要分情况讨论
(Ⅱ)思路一、一般地若任意
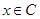 使得
使得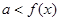 ,则
,则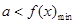 ;若任意
;若任意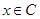 使得
使得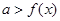 ,则
,则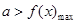 .由
.由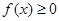 得:
得: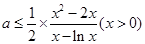 恒成立,所以
恒成立,所以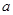 小于等于
小于等于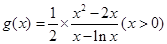 的最小值.
的最小值.思路二、除
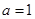 外,
外,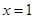 是
是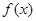 的一个极值点,故可首先考虑
的一个极值点,故可首先考虑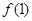 这个特殊值.由
这个特殊值.由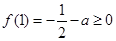 得:
得: 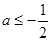 ,这样只需考虑
,这样只需考虑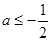 时
时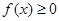 在
在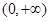 内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度.
内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度.试题解析:(Ⅰ)
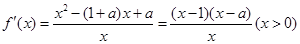
当
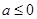 时,
时,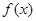 在
在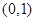 单调递减,在
单调递减,在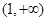 上单调递增;
上单调递增;当
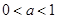 时,
时,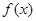 在
在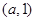 单调递减,在
单调递减,在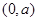 ,
,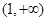 上单调递增;
上单调递增;当
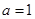 时,
时,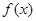 在
在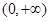 上单调递增;
上单调递增;当
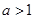 时,
时,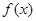 在
在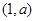 单调递减, 在
单调递减, 在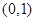 ,
,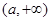 上单调递增.
上单调递增.(Ⅱ)法一、由
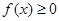 得:
得: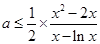
令
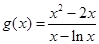 ,则
,则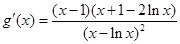
令
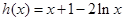 ,则
,则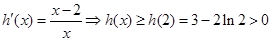 即
即
所以由
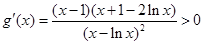 得
得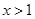
所以
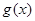 在
在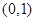 内单调递减,在
内单调递减,在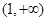 内单调递增.所以
内单调递增.所以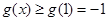
从而
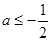
法二、由
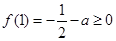 得:
得: 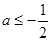
又
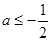 时,
时, 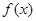 在
在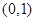 单调递减,在
单调递减,在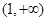 上单调递增
上单调递增所以即:
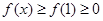
所以若
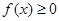 在
在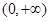 内恒成立,实数
内恒成立,实数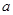 的取值范围为
的取值范围为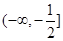 .
.
练习册系列答案
相关题目
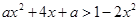 对一切
对一切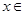 R恒成立,求实数
R恒成立,求实数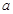 的取值范围;
的取值范围; 是定义在
是定义在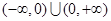 上的奇函数,当
上的奇函数,当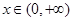 时,
时,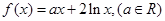 ,求
,求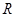 上的奇函数
上的奇函数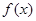 满足
满足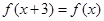 ,当
,当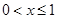 时,
时,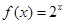 ,则
,则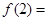 ( )
( )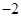
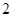
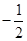
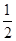
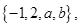 则
则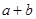 =___________.
=___________.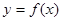 的最小正周期为
的最小正周期为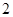 ,且
,且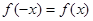 .当
.当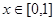 时
时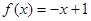 ,那么在区间
,那么在区间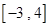 上,函数
上,函数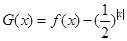 的零点个数( )
的零点个数( ) 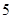
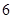
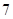
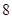
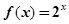
 可以表示为一个奇函数
可以表示为一个奇函数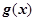 与一个偶函数
与一个偶函数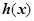 之和,若不等式
之和,若不等式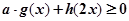 对于
对于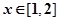 恒成立,则实数
恒成立,则实数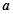 的取值范围是____________.
的取值范围是____________.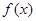 是定义在
是定义在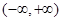 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数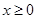 ,都有
,都有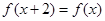 ,且当
,且当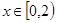 时,
时,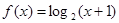 ,则
,则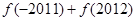 的值为 ( )
的值为 ( )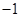

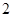
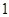
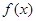 是定义域为实数集
是定义域为实数集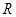 的偶函数,
的偶函数,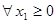 ,
,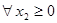 ,若
,若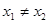 ,则
,则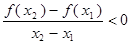 .如果
.如果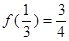 ,
,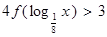 ,那么
,那么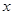 的取值范围为( )
的取值范围为( )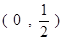
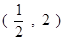
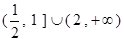
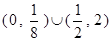
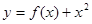 是奇函数,且
是奇函数,且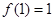 .若
.若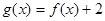 ,则
,则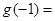 _______ .
_______ .