题目内容
圆(x+1)2+y2=4上的动点p到直线x+y-7=0的距离的最小值等于( )
分析:求出圆心到直线x+y-7=0的距离d,由d-r即可求出P到直线距离的最小值.
解答:解:由圆方程得:圆心(-1,0),半径r=2,
∵圆心到直线x+y-7=0的距离d=
=4
,
∴动点P到直线x+y-7=0的距离的最小值等于d-r=4
-2.
故选A.
∵圆心到直线x+y-7=0的距离d=
| |-1+0-7| | ||
|
| 2 |
∴动点P到直线x+y-7=0的距离的最小值等于d-r=4
| 2 |
故选A.
点评:此题考查了直线与圆的位置关系,点到直线的距离公式,圆的标准方程,根据题意得出动点P到直线x+y-7=0的距离的最小值为d-r是解本题的关键.

练习册系列答案
相关题目
过点(3,1)作一直线与圆(x-1)2+y2=9相交于M、N两点,则|MN|的最小值为( )
A、2
| ||
| B、2 | ||
| C、4 | ||
| D、6 |
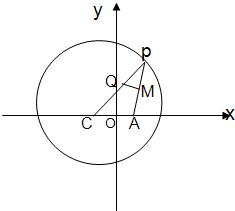 已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且