题目内容
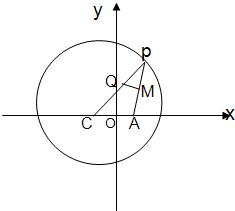 已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且| MQ |
| AP |
| AP |
| AM |
(1)当点P在圆上运动时,求点Q的轨迹方程;
(2)设过点(0,2)且斜率为2的直线l与(1)中所求的曲线交于B,D两点,O为坐标原点,求△BDO的面积.
分析:(1)把题中条件转化为MQ是线段AP的垂直平分线,得出点Q的轨迹是以点C和点A为焦点,半焦距c=1,长半轴的a=
的椭圆即可点Q的轨迹方程;
(2)求出(0,0)到直线L的距离以及利用弦长公式求出|BD|的长即可求△BDO的面积.
| 2 |
(2)求出(0,0)到直线L的距离以及利用弦长公式求出|BD|的长即可求△BDO的面积.
解答:解:(1)由题得,MQ是线段AP的垂直平分线,故|QC|+|QA|=|QC|+|QP|=|CP|=2
>|CA|=2,
于是点Q的轨迹是以点C和点A为焦点,半焦距c=1,长半轴的a=
的椭圆,短半轴b=
=1.
所以点Q的轨迹方程是:
+y2=1..
(2)因直线L过点(0,2)且斜率为2,则直线方程为y=2x+2,即2x-y+2=0.
故点(0,0)到直线L的距离d=
=
..
把y=2x+2代入(1)中的方程
+y2=1,化简得9x2+16x+6=0.△=162-4×9×6=40>0
.设B(x1,y1),D(x2,y2),则x1+x2=-
,x1•x2=
.
∴|BD|=
|x1-x2|=
]=
.
故△BDO的面积S△BOD=
•|BD|•d=
.
| 2 |
于是点Q的轨迹是以点C和点A为焦点,半焦距c=1,长半轴的a=
| 2 |
| a2-b2 |
所以点Q的轨迹方程是:
| x2 |
| 2 |
(2)因直线L过点(0,2)且斜率为2,则直线方程为y=2x+2,即2x-y+2=0.
故点(0,0)到直线L的距离d=
| 2 | ||
|
2
| ||
| 5 |
把y=2x+2代入(1)中的方程
| x2 |
| 2 |
.设B(x1,y1),D(x2,y2),则x1+x2=-
| 16 |
| 9 |
| 2 |
| 3 |
∴|BD|=
| 1+ k2 |
5[(-
|
10
| ||
| 9 |
故△BDO的面积S△BOD=
| 1 |
| 2 |
2
| ||
| 9 |
点评:在求动点的轨迹方程问题时,一般是利用条件找到动点所在曲线或找到关于动点坐标的等式,可得动点的轨迹方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
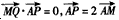 。
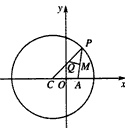
。
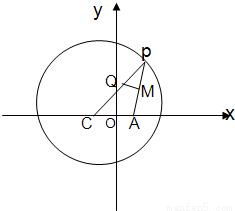 已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
已知点C为圆(x+1)2+y2=8的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且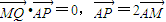 .
.