题目内容
(本题满分12分)
设 .
.
(1)求实数a;
(2)求数列{xn}的通项公式;
(3)若 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.
设
 .
.(1)求实数a;
(2)求数列{xn}的通项公式;
|
 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.解:(1) ;(2)
;(2) (3)见解析。
(3)见解析。
 ;(2)
;(2) (3)见解析。
(3)见解析。本试题主要是考出函数与方程的解,以及数列的递推关系的运用,求解通项公式,以及数列的和的总额和运用。
(1)先利用方程有唯一解,转换为关于一元二次方程只有一个解,利用判别式为零得到结论。
(2)根据递推关系式,取其倒数,然后分析得到等差数列的定义,求解通项公式。
(3)在上一问的前提下,得到通项公式可以裂项为两项,利用裂项法求和得到结论。
解:(1)由


(1)先利用方程有唯一解,转换为关于一元二次方程只有一个解,利用判别式为零得到结论。
(2)根据递推关系式,取其倒数,然后分析得到等差数列的定义,求解通项公式。
(3)在上一问的前提下,得到通项公式可以裂项为两项,利用裂项法求和得到结论。
解:(1)由




练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 个连续自然数按规律排成下表,根据规律,2011到2013,箭头的方向依次为( )
个连续自然数按规律排成下表,根据规律,2011到2013,箭头的方向依次为( )
 的前
的前 项和
项和 ,则
,则 ________________;
________________;
 的前n项和为 ____________.
的前n项和为 ____________. 的各项按如下规律排列:
的各项按如下规律排列: .
. ,
, ,
,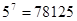 ,…,则
,…,则 的末四位数字为 .
的末四位数字为 .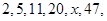 …中的
…中的 等于( )
等于( )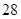
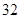


 }中,
}中,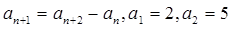 ,则
,则 为( )
为( )