Question

如图，在直三棱柱ABC－A₁B₁C₁中，∠ACB＝90°，A₁B₁＝2，A₁C₁＝1，D为棱CC₁的中点，B₁C⊥BD，

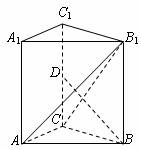
   （1）求证：AB₁⊥BD；

   （2）求直三棱柱的全面积S．

Answer 1

证明: (1)在直三棱柱ABC－A₁B₁C₁中，CC₁⊥平面ABC，

所以CC₁⊥AC，又AC⊥BC，BC∩CC₁＝C，

所以AC⊥平面BCC₁B₁，所以AC⊥BD，

又BD⊥B₁C，B₁C∩AC＝C，所以BD⊥平面AB₁C，所以AB₁⊥BD．

(2)解:在Rt△ABC中，AC＝1，AB＝2，所以BC＝．

在矩形BCC₁B₁中，△BCD∽△B₁BC，所以＝，又BB₁＝2CD，

所以BB₁＝．S＝S_侧＋2S_△ABC＝BB₁(AB＋BC＋AC)＋2××1×＝3＋3＋．